
 如图,以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上一点M为圆心的圆恰好与y轴相切,与x轴交于A,B两点,其中A是双曲线的右顶点,若△MAB是等边三角形,则该双曲线的离心率是( )
如图,以双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上一点M为圆心的圆恰好与y轴相切,与x轴交于A,B两点,其中A是双曲线的右顶点,若△MAB是等边三角形,则该双曲线的离心率是( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 利用M为圆心的圆恰好与y轴相切,与x轴交于A,B两点,其中A是双曲线的右顶点,若△MAB是等边三角形,得出M(2a,$\sqrt{3}$a),代入双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,即可求出双曲线的离心率.
解答 解:∵M为圆心的圆恰好与y轴相切,与x轴交于A,B两点,其中A是双曲线的右顶点,若△MAB是等边三角形,
∴M(2a,$\sqrt{3}$a),
代入双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,可得$\frac{4{a}^{2}}{{a}^{2}}-\frac{3{a}^{2}}{{b}^{2}}$=1,
∴a=b,
∴c=$\sqrt{2}a$,
∴$e=\frac{c}{a}=\sqrt{2}$.
故选:C.
点评 本题考查双曲线的离心率的求法,考查化简整理的运算能力,确定M的坐标是关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [8,+∞) | C. | (-∞,-1]∪[8,+∞) | D. | (-1,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
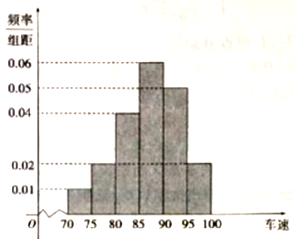 师大附中高一研究性学习小组,在某一高速公路服务区,从小型汽车中按进服务区的先后,以每间隔10辆就抽取一辆的抽样方法抽取20名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100]统计后得到如图的频率分布直方图.
师大附中高一研究性学习小组,在某一高速公路服务区,从小型汽车中按进服务区的先后,以每间隔10辆就抽取一辆的抽样方法抽取20名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100]统计后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{e}$ | B. | 2e2 | C. | 2e | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com