
分析 因为|$\overrightarrow{e}$|=1,$\overrightarrow{a}$•$\overrightarrow{e}$=1,$\overrightarrow{b}$•$\overrightarrow{e}$=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,所以$\overrightarrow{e}$•|$\overrightarrow{a}$+$\overrightarrow{b}$|=3,设$\overrightarrow{e}$与|$\overrightarrow{a}$+$\overrightarrow{b}$|的夹角为θ[0,π),利用三角函数的有界限求其最小值.因为|$\overrightarrow{e}$|=1,不妨设坐标为$\overrightarrow{e}$(1,0),$\overrightarrow{a}$•$\overrightarrow{e}$=1,$\overrightarrow{b}$•$\overrightarrow{e}$=2,可设为$\overrightarrow{a}$(1,m),$\overrightarrow{b}$(2,n),利用,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,求出n,m的关系,即可得到$\overrightarrow{a}$•$\overrightarrow{b}$的最小值.
解答 解:由题意:∵|$\overrightarrow{e}$|=1,$\overrightarrow{a}$•$\overrightarrow{e}$=1,$\overrightarrow{b}$•$\overrightarrow{e}$=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
∴$\overrightarrow{e}$•|$\overrightarrow{a}$+$\overrightarrow{b}$|=3,
设$\overrightarrow{e}$与|$\overrightarrow{a}$+$\overrightarrow{b}$|的夹角为θ[0,π),
则|$\overrightarrow{a}$+$\overrightarrow{b}$|$•|\overrightarrow{e}|•cosθ$=3,
那么:|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\frac{3}{cosθ}$(θ∈[0,π))
当cosθ=1时,即θ=0°时,
|$\overrightarrow{a}$+$\overrightarrow{b}$|的最小值为3.
∵|$\overrightarrow{e}$|=1,不妨设坐标为$\overrightarrow{e}$(1,0),$\overrightarrow{a}$•$\overrightarrow{e}$=1,$\overrightarrow{b}$•$\overrightarrow{e}$=2,可设为$\overrightarrow{a}$(1,m),$\overrightarrow{b}$(2,n),
那么:$\overrightarrow{a}$-$\overrightarrow{b}$=(-1,m-n)
∵|$\overrightarrow{a}$-$\overrightarrow{b}$|=2
∴$\sqrt{1+(m-n)^{2}}=2$
∴(m+n)2=3+4mn≥0
∴$mn≥-\frac{3}{4}$
当且仅m=-n=$±\frac{\sqrt{3}}{2}$时取等号.
则$\overrightarrow{a}$•$\overrightarrow{b}$=2+mn$≥2-\frac{3}{4}=\frac{5}{4}$
故答案为:3,$\frac{5}{4}$.
点评 本题考查了数量积运算性质与三角函数的性质的结合,考查了推理能力与计算能力,属于中档题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
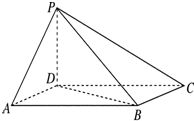 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [156,160) | ||
| [160,164) | 4 | |
| [164,168) | 12 | |
| [168,172) | 12 | |
| [172,176) | 0.26 | |
| [176,180] | 6 | |
| 合计 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com