
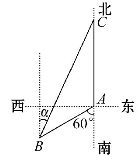
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度.
(2)求sinα的值.
(1)14海里/小时 (2)
【解析】(1)依题意,∠BAC=120°,AB=12,AC=10×2=20,∠BCA=α.
在△ABC中,由余弦定理,得
BC2=AB2+AC2-2AB×AC×cos∠BAC
=122+202-2×12×20×cos120°=784.
解得BC=28.
所以渔船甲的速度为 =14海里/小时.
=14海里/小时.
(2)方法一:在△ABC中,因为AB=12,∠BAC=120°,BC=28,∠BCA=α,
由正弦定理,得 =
= .
.
即sinα= =
= =
= .
.
方法二:在△ABC中,因为AB=12,AC=20,BC=28,∠BCA=α,由余弦定理,得cosα= ,即cosα=
,即cosα= =
= .
.
因为α为锐角,所以sinα= =
= =
= .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源:2014年高考数学人教版评估检测 第八章 平面解析几何(解析版) 题型:选择题
若双曲线 -
- =1(a>0,b>0)上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
=1(a>0,b>0)上不存在点P使得右焦点F关于直线OP(O为双曲线的中心)的对称点在y轴上,则该双曲线离心率的取值范围为( )
A.( ,+∞) B.[
,+∞) B.[ ,+∞)
,+∞)
C.(1, ] D.(1,
] D.(1, )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第二章 函数、导数及其应用(解析版) 题型:填空题
(2014·鄂州模拟)已知幂函数f(x)=x2+m是定义在区间[-1,m]上的奇函数,则f(m+1)=__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(解析版) 题型:填空题
(2014·沈阳模拟)甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别 射击了5次,成绩如下表(单位:环):
射击了5次,成绩如下表(单位:环):
甲 | 10 | 8 | 9 | 9 | 9 |
乙 | 10 | 10 | 7 | 9 | 9 |
如果甲、乙两人中只有1人入选,那么入选的最佳人选应是__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(解析版) 题型:选择题
(2014·仙桃模拟)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )

A.65辆 B.76辆 C.88辆 D.95辆
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:填空题
在△ABC中,a=2,则b·cosC+c·cosB的值为__________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:选择题
(2014·天门模拟)若函数f(x)=sinωx+ cosωx,x∈R,又f(α)=-2,f(β)=0,且|α-β|的最小值为
cosωx,x∈R,又f(α)=-2,f(β)=0,且|α-β|的最小值为 ,则正数ω的值为( )
,则正数ω的值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:填空题
如图所示是一个正方体的表面展开图,A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com