
分析 (1)求导数,确定切线的斜率,即可求函数g(x)在(0,1)处的切线方程;
(2)h(x)=g(x)-a(x3+x2)=0,可得a=$\frac{{e}^{x}}{{x}^{2}}$,确定函数的单调性,可得函数的极小值,即可得出结论.
解答 解:(1)g′(x)=ex(x+2),g′(0)=2,
∴函数g(x)在(0,1)处的切线方程为y-1=2x,即l:y=2x+1(4分)
(2)h(x)=g(x)-a(x3+x2)=0,可得a=$\frac{{e}^{x}}{{x}^{2}}$,
设y=$\frac{{e}^{x}}{{x}^{2}}$,则y′=$\frac{{e}^{x}(x-2)}{{x}^{3}}$,函数在(0,2)上单调递减,(2,+∞)上单调递增,
∴x=2函数取得极小值$\frac{{e}^{2}}{4}$,
∴$a=\frac{e^2}{4}$,零点1个; $a>\frac{e^2}{4}$,零点2个;$0<a<\frac{e^2}{4}$,零点0个 (8分)
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性的运用,属于中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{7π}{12}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 540 | B. | -540 | C. | 135 | D. | -135 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | 16 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
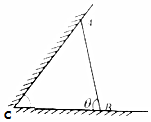 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点D不在直线BC上 | B. | 点D在BC的延长线上 | ||
| C. | 点D在线段BC上 | D. | 点D在CB的延长线上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com