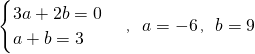Question

已知函数f（x）=ax³+bx²，当x=1时，有极大值3；
（Ⅰ）求a，b的值．
（Ⅱ）若点P是函数图象上的一点，横坐标为-1，求过P点的切线方程．

Answer 1

解：（I）y′=3ax²+2bx，当x=1时，y′|_x=1=3a+2b=0，y|_x=1=a+b=3，
即
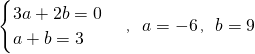
（II）：由（I）得：
f（x）=-6x³+9x²
∴P点的坐标为P（-1，15）
∵f′（x）=-18x²+18x，
设切点坐标为（t，-6t³+9t²），切线斜率为：f′（t）=-18t²+18t
则切线方程为y-（-6t³+9t²）=（-18t²+18t）（x-t），
∵切线过点P（-1，15），
∴15-（-6t³+9t²）=（-18t²+18t）（x+1），
化简得t³-3t²=0，∴t=0或t=3．
∴切线的方程：3x+y=0或24x-y-54=0．
分析：（I）求出y′，由x=1时，函数有极大值3，所以代入y和y′=0中得到两个关于a、b的方程，求出a、b即可；
（II）欲求出切线方程，只须求出其斜率即可，故先设切点坐标为（t，t³-3t），利用导数求出在x=t处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．
点评：考查学生利用导数研究函数极值的能力，以及会用待定系数法求函数解析式的能力．本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力．属于基础题．