
����Ŀ��ij�̳������н���������˿���һ��������Ʒ�ɳ齱���齱�������£�1���齱�������������֣�����![]() ����װ��1������2��������ɫ��ͬ���ļ״����������1�������Ǻ������ý���15Ԫ������û�н��𣬶ҽ�����������Żؼ״��У�����
����װ��1������2��������ɫ��ͬ���ļ״����������1�������Ǻ������ý���15Ԫ������û�н��𣬶ҽ�����������Żؼ״��У�����![]() ����װ��2���졢1��������ɫ��ͬ�����Ҵ����������1�������Ǻ������ý���10Ԫ������û�н��𣬶ҽ�����������Ż��Ҵ��С�
����װ��2���졢1��������ɫ��ͬ�����Ҵ����������1�������Ǻ������ý���10Ԫ������û�н��𣬶ҽ�����������Ż��Ҵ��С�
�齱�����ǣ��˿�����Ʒ�Ľ����100Ԫ���ɸ��ݷ���![]() �齱һ������150Ԫ���ɸ��ݷ���
�齱һ������150Ԫ���ɸ��ݷ���![]() �齱������ij�˿�����Ʒ�Ľ��Ϊ310Ԫ����ù˿Ͳ��õij齱��ʽ�������������֣����ݷ���
�齱������ij�˿�����Ʒ�Ľ��Ϊ310Ԫ����ù˿Ͳ��õij齱��ʽ�������������֣����ݷ���![]() �齱���λ�
�齱���λ�![]() �齱���λ�
�齱���λ�![]() ���齱һ�Σ�����֪�˿�
���齱һ�Σ�����֪�˿�![]() �ڸ��̳�������Ʒ�Ľ��Ϊ250Ԫ��
�ڸ��̳�������Ʒ�Ľ��Ϊ250Ԫ��
��1�����˿�![]() ֻѡ����ݷ���
ֻѡ����ݷ���![]() ���г齱����������Ϊ15Ԫ�ĸ��ʣ�
���г齱����������Ϊ15Ԫ�ĸ��ʣ�
��2�������˿�![]() ����ÿ�ֳ齱��ʽ�Ŀ����Զ���ȣ��������п��ܻ�õĽ�������0Ԫ���⣩��
����ÿ�ֳ齱��ʽ�Ŀ����Զ���ȣ��������п��ܻ�õĽ�������0Ԫ���⣩��
���𰸡�(1) ![]() ��(2)15Ԫ.
��(2)15Ԫ.
�����������������
(1)�������г����п��ܵ��¼���Ȼ���Ϲŵ���ͼ��㹫ʽ�ɵ�����Ϊ15Ԫ�ĸ�����![]() ��
��
(2)������������ַ����������ۿɵ������п��ܻ�õĽ�������15Ԫ.
���������
��1���Ǽ״��к�����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]()
������ù˿�![]() ���ԴӼ״����Ⱥ�����2���������еȿ��ܳ��ֵĽ��Ϊ
���ԴӼ״����Ⱥ�����2���������еȿ��ܳ��ֵĽ��Ϊ
![]() ��9�֣�
��9�֣�
���н��![]() �ɻ�15Ԫ�����Թ˿�
�ɻ�15Ԫ�����Թ˿�![]() ����Ϊ15Ԫ�ĸ���Ϊ
����Ϊ15Ԫ�ĸ���Ϊ![]() .
.
��2��������Ĺ˿�![]() ���Ը��ݷ���
���Ը��ݷ���![]() �齱���λ���ݷ���
�齱���λ���ݷ���![]() ���齱һ�Ρ��ɣ�1��֪�˿�
���齱һ�Ρ��ɣ�1��֪�˿�![]() ���ݷ���
���ݷ���![]() �齱����������������1��
�齱����������������1��
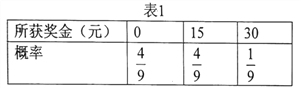
���Ҵ��к���ֱ���![]() ������
������![]()
��˿�![]() ���ݷ���
���ݷ���![]() ���齱һ�ε����еȿ��ܳ��ֵĽ��Ϊ
���齱һ�ε����еȿ��ܳ��ֵĽ��Ϊ
![]() ��9��
��9��
���н��![]() �ɻ�25Ԫ�����
�ɻ�25Ԫ�����![]() �ɻ�15Ԫ��
�ɻ�15Ԫ��
![]() �ɻ�10Ԫ������ɻ�0Ԫ�����Թ˿�
�ɻ�10Ԫ������ɻ�0Ԫ�����Թ˿�![]() ���ݷ���
���ݷ���![]() ���齱һ��������������2��
���齱һ��������������2��

�ɱ�1����2��֪�˿�![]() ���п��ܻ�õĽ�����Ϊ15Ԫ.
���п��ܻ�õĽ�����Ϊ15Ԫ.


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4λͬѧ��ͬһ����ϡ�����μӡ����������ء�����������Զ�������λ�������������������̨�ס������Ŀ�IJ��ԣ�ÿλͬѧ�ϡ����������һ����Ŀ���Ҳ��ظ��������粻�⡰��������Ŀ�����粻�⡰̨�ס���Ŀ��������Ŀ�ϡ����綼������һ�ˣ���ͬ�İ��ŷ�ʽ����__________�֣����������𣩣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x������f��x��+f��2��x��=2����x�ʣ�0��1]ʱ��f��x��=x2 �� ��x�ʣ���1��0]ʱ�� ![]() ���������ڣ���1��3���ϵĺ���g��x��=f��x����t��x+1����������ͬ����㣬��ʵ��t��ȡֵ��Χ�ǣ� ��
���������ڣ���1��3���ϵĺ���g��x��=f��x����t��x+1����������ͬ����㣬��ʵ��t��ȡֵ��Χ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��ѡ��ȫ���������С�����200��־Ը���������ȡ40��־Ը�߲μӽֵ������ල�������ͳ����Щ־Ը�ߵ��������25���55��֮�䣬Ϊ���㰲����������־Ը�߰������С����ֳ����飬����Ϊ![]() ����ͼ�ǰ����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪������
����ͼ�ǰ����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪������![]() ������Ϊ4��.
������Ϊ4��.
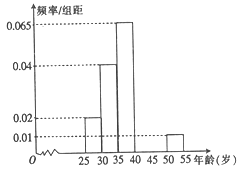
��1����������Ƶ�ʲ�����200��־Ը����������40������(��40�꣩��������
��2����������λ�ڵ�����͵������־Ը���������ȡ�����������ǵ�����ֱ�Ϊ![]() ���¼�
���¼�![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȡij��ѧ�ס��������10��ͬѧ���������ǵ����ߣ���λ��cm��������������ݵľ�Ҷͼ��ͼ7.

��1�����ݾ�Ҷͼ�ж��ĸ����ƽ�����߽ϸߣ�
��2������װ���������
��3���ִ��Ұ���10��ͬѧ�������ȡ�������߲�����173cm��ͬѧ��������Ϊ176cm��ͬѧ�����еĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������������Ϸ�����ɼ�����һ�����ּ�Ϊa�������Ҳ¼ղ�������֣�����������ּ�Ϊb����a��b��{1��2��3��4��5��6}���Ǧ�=|a��b|��
��1�����=1�ĸ��ʣ�
��2�����Ρ�1����ơ�����������Ϭ��������������Ϭ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У�
�� ![]() ����
����![]() Ϊ
Ϊ![]() �����ģ�
�����ģ� ![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() ƽ��
ƽ��![]() ����ֱ��
����ֱ��![]() ��
��![]() ���ɽǵ�����ֵΪ__________��
���ɽǵ�����ֵΪ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com