
分析 由曲线y=f(x)在点(1,f(1))处的切线垂直于直线x-3y=0可得f′(1)=-3,可求出a的值,可得切点坐标,即可求出切线方程.
解答 解:∵f(x)=$\frac{x}{4}$+$\frac{a}{x}$-lnx-$\frac{3}{2}$,
∴f′(x)=$\frac{1}{4}-\frac{a}{{x}^{2}}-\frac{1}{x}$,
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线x-3y=0,
∴f′(1)=$\frac{1}{4}$-a-1=-3,
解得:a=$\frac{9}{4}$,
∴f(1)=1,
∴切线方程为y-1=-3(x-1),即3x+y-4=0.
故答案为:3x+y-4=0.
点评 本题考查的知识点是利用导数研究曲线上某点切线方程,求出a是关键,难度中档.


科目:高中数学 来源: 题型:解答题
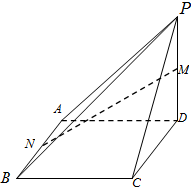 如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.
如图:在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=DA=DC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com