
分析 $e=\frac{c}{a}=\frac{\sqrt{2}}{2}$,可得a=$\sqrt{2}$c=$\sqrt{2}$b.因此椭圆的方程化为:x2+2y2=2c2.把x=c代入椭圆方程解得y,不妨取M$(c,\frac{\sqrt{2}c}{2})$,由于CD⊥OM,可得kCD=-$\sqrt{2}$.直线CD的方程为:y=-$\sqrt{2}$(x-c).设C(x1,y1),D(x2,y2).与椭圆方程联立化为:5x2-8cx+2c2=0,利用根与系数的关系可得|CD|=$\sqrt{3[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$.求出点F1(-c,0)到直线CD的距离d,利用${S}_{△{F}_{1}CD}$=$\frac{1}{2}$d|CD|=20$\sqrt{3}$,解出即可得出.
解答 解:∵$e=\frac{c}{a}=\frac{\sqrt{2}}{2}$,∴a=$\sqrt{2}$c=$\sqrt{2}$b.因此椭圆的方程化为:x2+2y2=2c2.
把x=c代入椭圆方程可得:c2+2y2=2c2,解得y=±$\frac{c}{\sqrt{2}}$,不妨取M$(c,\frac{\sqrt{2}c}{2})$,
∴kOM=$\frac{\sqrt{2}}{2}$,∴kCD=-$\sqrt{2}$.
∴直线CD的方程为:y=-$\sqrt{2}$(x-c).设C(x1,y1),D(x2,y2).
联立$\left\{\begin{array}{l}{y=-\sqrt{2}(x-c)}\\{{x}^{2}+2{y}^{2}=2{c}^{2}}\end{array}\right.$,化为:5x2-8cx+2c2=0,
∴x1+x2=$\frac{8c}{5}$,x1•x2=$\frac{2{c}^{2}}{5}$,
∴|CD|=$\sqrt{3[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{3(\frac{64{c}^{2}}{25}-4×\frac{2{c}^{2}}{5})}$=$\frac{6\sqrt{2}c}{5}$.
点F1(-c,0)到直线CD的距离d=$\frac{|\sqrt{2}c+\sqrt{2}c|}{\sqrt{3}}$=$\frac{2\sqrt{6}c}{3}$,
∴${S}_{△{F}_{1}CD}$=$\frac{1}{2}$d|CD|=$\frac{1}{2}$×$\frac{2\sqrt{6}c}{3}$×$\frac{6\sqrt{2}c}{5}$=20$\sqrt{3}$,
解得c2=150.
∴a2=300,b2=150.
∴椭圆的标准方程为:$\frac{{x}^{2}}{300}$+$\frac{{y}^{2}}{150}$=1.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次的根与系数的关系、弦长公式、点到直线的距离公式,考查了推理能力与计算能力,属于难题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“幂函数f(x)=(m2-m-1)xm在(0,+∞)上为增函数,则m=-1”为真命题 | |
| C. | 命题“若x=y则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
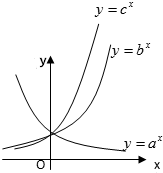
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com