
���� ��1�������귽������ͬ�˦ѣ����ݼ�������ֱ������Ķ�Ӧ��ϵ���ɵó���ͨ���̣�
��2����ֱ�ߵIJ������̴�������C����ͨ���̵ó�P��Q��Ӧ�IJ������Ӷ����|yP-yQ|�����������ʽ�ó��������m�ĺ�����ʹ�û�Ԫ�����õ�������ú����ĵ����ԣ��Ӷ��ó���������ֵ��
��� �⣺��1���ɦ�=4cos�ȵæ�2=4��cos�ȣ�
�Ѧ�2=x2+y2����cos��=x������ʽ��x2+y2-4x=0������x-2��2+y2=4��
������C��ʾ�ԣ�2��0��ΪԲ�ģ���2Ϊ�뾶��Բ��
��2����$\left\{{\begin{array}{l}{x=1+2mt}\\{y=2t\;\;\;\;\;\;\;}\end{array}}\right.$����x2+y2-4x=0��4��1+m2��t2-4mt-3=0��
��P��Q��Ӧ�IJ����ֱ�Ϊt1��t2����t1t2=-$\frac{3}{4��1+{m}^{2}��}$��t1+t2=$\frac{m}{1+{m}^{2}}$��
��|yP-yQ|=|2t1-2t2|=2|t1-t2|=2$\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}$=$\frac{2\sqrt{4{m}^{2}+3}}{1+{m}^{2}}$��
��M��1��0������S��OPQ=S��OMP+S��OMQ=$\frac{1}{2}$|OM||yP-yQ|=$\frac{\sqrt{4{m}^{2}+3}}{1+{m}^{2}}$��
��$\sqrt{4{m}^{2}+3}$=t����t��$\sqrt{3}$��m2=$\frac{{t}^{2}-3}{4}$��
��S��OPQ=$\frac{4t}{{t}^{2}+1}$����f��t��=$\frac{4t}{{t}^{2}+1}$����f�䣨t��=$\frac{1-4{t}^{2}}{��1+{t}^{2}��^{2}}$��0��
��f��t����[$\sqrt{3}$��+�ޣ���Ϊ��������
�൱t=$\sqrt{3}$ʱ��f��t��ȡ�����ֵf��$\sqrt{3}$��=$\sqrt{3}$��
�൱t=$\sqrt{3}$��m=0ʱ����OPQ�����ȡ�����ֵ$\sqrt{3}$��
���� ���⿼���˼����귽������ͨ���̵�ת����ֱ����Բ��λ�ù�ϵ��������ֵ���������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-3��2+��y-4��2=25 | B�� | ��x-3��2+��y-4��2=20 | C�� | ��x-3��2+��y-4��2=26 | D�� | ��x-3��2+��y-4��2=27 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -10 | B�� | 4 | C�� | 10 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
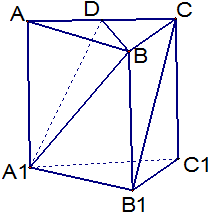 ��֪��������ABC-A1B1C1��D��AC���е㣬��֤��
��֪��������ABC-A1B1C1��D��AC���е㣬��֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
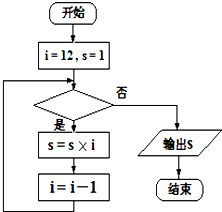
| A�� | i��10�� | B�� | i��11�� | C�� | i��12�� | D�� | i��11�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com