
| A. | (x-3)2+(y-4)2=25 | B. | (x-3)2+(y-4)2=20 | C. | (x-3)2+(y-4)2=26 | D. | (x-3)2+(y-4)2=27 |
分析 分别求圆心到三点的距离分别为5,2$\sqrt{5}$,$\sqrt{26}$,则圆的半径为中间的那个数,则可得圆的方程.
解答 解:∵圆心M(3,4),点A(-1,1),B(1,0),C(-2,3),
∴MA=$\sqrt{(3+1)^{2}+(4-1)^{2}}$=5,
MB=$\sqrt{(3-1)^{2}+(4-0)^{2}}$=2$\sqrt{5}$,
MC=$\sqrt{(3+2)^{2}+(4-3)^{2}}$=$\sqrt{26}$,
要使A,B,C三点一个在圆内,一个在圆上,一个在圆外
即使R=5
∴圆方程为(x-3)2+(y-4)2=25.
故选:A.
点评 本题考查圆的方程的求法,是基础题,解题时要注意两点间距离公式的合理运用.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
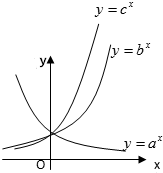
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | -$\frac{{\sqrt{5}}}{3}$ | D. | ±$\frac{{\sqrt{5}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价 格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量y | 12 | 10 | 7 | 5 | 3 |
| n-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 | 0.874 | 0.834 | 0.798 | 0.765 | 0.735 | 0.708 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com