
分析 (Ⅰ)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的极值即可;
(Ⅱ)设出P点的坐标,求出坐标,代入切线方程即可;
(Ⅲ)设$g(x)=-30(x-\root{5}{6})$,令F(x)=f(x)-g(x),设方程g(x)=a的根为${x_2}^'$,设方程h(x)=a的根为${{x}_{1}}^{′}$,根据函数的单调性求出x2-x1≤${{x}_{2}}^{′}$-${{x}_{1}}^{′}$,从而证出结论.
解答 解:(Ⅰ)由已知得:f′(x)=6(1-x5) 由f′(x)=0得:x=1
又 当x<1时,f′(x)>0,f(x)单调递增,
当x>1时,f′(x)<0,f(x)单调递减,
∴当x=1时f(x)取得极大值,极大值为f(1)=5,无极小值.…(3分)
(Ⅱ)设P(x0,0),则${x_0}=\root{5}{6}$,f'(x0)=-30,
曲线f(x)在点P处的切线方程为:$y=f'({x_0})({x-{x_0}})=-30(x-\root{5}{6})$,
即 曲线在点P处的切线方程为:$y=-30(x-\root{5}{6})$…(6分)
(Ⅲ)设$g(x)=-30(x-\root{5}{6})$,令F(x)=f(x)-g(x)
即$F(x)=f(x)+30(x-\root{5}{6})$,则F'(x)=f'(x)+30
由于f′(x)=6-6x5在R 单调递减,故F′(x)在R 单调递减,又∵F′(x0)=0,$({x_0}=\root{5}{6})$
∴当x∈(-∞,x0)时F'(x)>0,当x∈(x0,+∞)时,F′(x)<0,
∴F(x) 在(-∞,x0)单调递增,在(x0,+∞)单调递减,
∴?x∈R,F(x)≤F(x0)=0,即?x∈R,都有f(x)≤g(x);
设方程g(x)=a的根为${x_2}^'$,∴${{x}_{2}}^{′}$=${6}^{\frac{1}{5}}$-$\frac{a}{30}$.
∵g(x)在R 单调递减,且g(x2)≥f(x2)=a=g(${{x}_{2}}^{′}$)
∴x2<${{x}_{2}}^{′}$,
设曲线y=f(x) 在点原点处的切线方程为:y=h(x),则易得h(x)=6x,
?x∈R,有f(x)-h(x)=-x6≤0,即f(x)≤h(x),
设方程h(x)=a的根为${{x}_{1}}^{′}$,则${{x}_{1}}^{′}$=$\frac{a}{6}$,
∵h(x)在R 单调递增,且h(${{x}_{1}}^{′}$)=a=f(x1)≤h(x1),
∴${{x}_{1}}^{′}$≤x1
∴x2-x1≤${{x}_{2}}^{′}$-${{x}_{1}}^{′}$=(${a}^{\frac{1}{5}}$-$\frac{a}{30}$)-$\frac{a}{6}$=${a}^{\frac{1}{5}}$-$\frac{a}{5}$,
即x2-x1≤${a}^{\frac{1}{5}}$-$\frac{a}{5}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,考查曲线的切线方程问题,是一道综合题.


科目:高中数学 来源: 题型:解答题
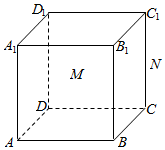 在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为A1B1,C1C的中点.
在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为A1B1,C1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
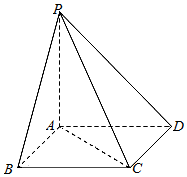 如图,四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,AB=$\sqrt{3}$,BC=1,PA=2.求:
如图,四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,AB=$\sqrt{3}$,BC=1,PA=2.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{13}{4}$ | C. | $\frac{15}{4}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com