
【题目】已知函数![]() (
(![]() ,
,![]() ),
),![]()
![]() (
(![]() ).
).
(1)如果![]() 是关于
是关于![]() 的不等式
的不等式![]() 的解,求实数
的解,求实数![]() 的取值范围;
的取值范围;
(2)判断![]() 在
在![]() 和
和![]() 的单调性,并说明理由;
的单调性,并说明理由;
(3)证明:函数![]() 存在零点q,使得
存在零点q,使得![]() 成立的充要条件是
成立的充要条件是![]() .
.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图半圆![]() 的直径为4,
的直径为4,![]() 为直径
为直径![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 为半圆周上任一点,以
为半圆周上任一点,以![]() 为边作等边
为边作等边![]() (
(![]() 、
、![]() 、
、![]() 按顺时针方向排列)
按顺时针方向排列)
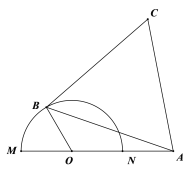
(1)若等边![]() 边长为
边长为![]() ,
,![]() ,试写出
,试写出![]() 关于
关于![]() 的函数关系;
的函数关系;
(2)问![]() 为多少时,四边形
为多少时,四边形![]() 的面积最大?这个最大面积为多少?
的面积最大?这个最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产A种型号的电脑.2013年平均每台电脑的生产成本为5000元,并按纯利润为20%定出厂价,2014年开始,公司更新设备,加强管理,逐步推行股份制,从而使生产成本逐年降低,2017年平均每台A种型号的电脑出厂价仅是2013年的80%,实现了纯利润50%.
(1)求2017年每台A种型号电脑的生产成本;
(2)以2013年的生产成本为基数,用二分法求2013-2017年间平均每年生产成本降低的百分率(精确度001).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,当x>0时满足:①f(x)﹣2f(﹣x)=0;②对任意x1>0,x2>0,x1≠x2有(x1﹣x2)(f(x1)﹣f(x2))>0恒成立:③f(4)=2f(2)=2,则不等式x[f(x)﹣1]>0的解集为_____(用区间表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生对“两个一百年”奋斗目标、实现中华民族伟大复兴中国梦的“关注度”(单位:天),某中学团委组织学生在十字路口采用随机抽样的方法抽取了80名青年学生(其中男女人数各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组青年学生的月“关注度”分为6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)现从“关注度”在![]() 的男生与女生中选取3人,设这3人来自男生的人数为
的男生与女生中选取3人,设这3人来自男生的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)在抽取的80名青年学生中,从月“关注度”不少于25天的人中随机抽取2人,求至少抽取到1名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)令![]() ,将函数
,将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)在(1)的条件下的函数![]() 的图像,区间
的图像,区间![]()
![]() 且
且![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点,在所有满足上述条件的
上至少含有30个零点,在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com