
已知函数f(x)=cos(2x+ )+sin2x
)+sin2x
(1)求函数f(x)的单调递减区间及最小正周期;
(2)设锐角△ABC的三内角A,B,C的对边分别是a,b,c,若c= ,cosB=
,cosB=
 求b.
求b.
(1)最小正周期T=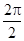 =π,f(x)的单调递减区间是[kπ-
=π,f(x)的单调递减区间是[kπ-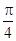 ,kπ+
,kπ+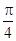 ](k∈Z).
](k∈Z).
(2) b=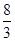 .
.
解析试题分析:(1)∵f(x)=cos(2x+ )+sin2x=cos2xcos
)+sin2x=cos2xcos -sin2xsin
-sin2xsin +
+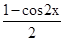
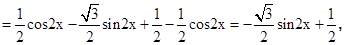
∴最小正周期T=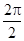 =π,令2kπ-
=π,令2kπ-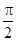 ≤2x≤2kπ+
≤2x≤2kπ+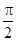 (k∈Z),得kπ-
(k∈Z),得kπ-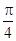 ≤x≤kπ+
≤x≤kπ+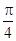 ,k∈Z,
,k∈Z,
∴f(x)的单调递减区间是[kπ-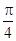 ,kπ+
,kπ+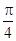 ](k∈Z).
](k∈Z).
(2)由(1)得f(x)=-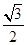 sin2x+
sin2x+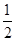 ,
,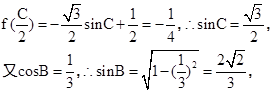
∴ 即
即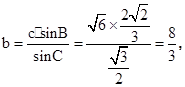 故b=
故b=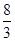 .
.
考点:本题主要考查三角函数的和差倍半公式,正弦定理的应用,三角函数的图象和性质。
点评:中档题,近些年,涉及三角函数、三角形的题目常常出现在高考题中,往往需要综合应用三角公式化简函数,以进一步研究函数的性质。应用正弦定理、余弦定理求边长、角等,有时运用函数方程思想,问题的解决较为方便。


科目:高中数学 来源: 题型:解答题
如图,在路边安装路灯,灯柱与地面垂直,灯杆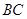 与灯柱
与灯柱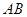 所在平面与道路垂直,且
所在平面与道路垂直,且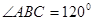 ,路灯
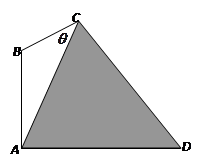
,路灯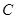 采用锥形灯罩,射出的光线如图阴影部分所示,已知
采用锥形灯罩,射出的光线如图阴影部分所示,已知 ,路宽
,路宽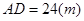 ,设灯柱高
,设灯柱高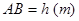 ,
,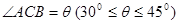 .
.
(1)求灯柱的高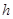 (用
(用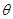 表示);
表示);
(2)若灯杆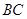 与灯柱
与灯柱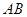 所用材料相同,记所用材料长度和为
所用材料相同,记所用材料长度和为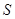 ,求
,求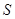 关于
关于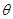 的函数表达式,并求出
的函数表达式,并求出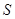 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知向量 ,函数
,函数 .
.
(1)求 的单调区间;
的单调区间;
(2)请说出 的图象是由
的图象是由 的图象经过怎样的变换得到的(说清每一步的变换方法);
的图象经过怎样的变换得到的(说清每一步的变换方法);
(3)当 时,求
时,求 的最大值及取得最大值时的
的最大值及取得最大值时的 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据市气象站对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(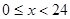 ,单位为小时,
,单位为小时, 表示气温,单位为摄氏度,
表示气温,单位为摄氏度,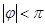 ,
,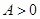 ),
),
现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高。
(1)求这条曲线的函数表达式;
(2)求这一天19时整的气温。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com