
 有一块直角三角形木板,如图所示,∠C=90°,AB=5cm,BC=3cm,AC=4cm.根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长.
有一块直角三角形木板,如图所示,∠C=90°,AB=5cm,BC=3cm,AC=4cm.根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长. 分析 由题意,设出正方形边长为a,根据勾股定理建立关系,利用相似三角形的性质求解边长的关系,即可求解最大值即可.
解答 解:如图(1)所示,设正方形DEFG的边长为x cm,过点C作CM⊥AB于M,交DE于N,
因为S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM,
所以AC•BC=AB•CM,即3×4=5•CM.所以CM=$\frac{12}{5}$.
因为DE∥AB,所以△CDE∽△CAB.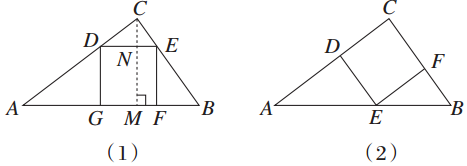
所以$\frac{CN}{CM}=\frac{DE}{AB}$,即$\frac{\frac{12}{5}-x}{\frac{12}{5}}=\frac{x}{5}$
所以x=$\frac{60}{37}$
如图(2)所示,设正方形CDEF的边长为y cm,因为EF∥AC,所以△BEF∽△BAC.
∴$\frac{BF}{BC}=\frac{EF}{AC}$,$\frac{3-x}{3}=\frac{y}{4}$.
∴y=$\frac{12}{7}$.
∵x=$\frac{60}{37}$,y=$\frac{12}{7}$,
∴x<y.
所以当按图(2)的方法裁剪时,正方形面积最大,其边长为$\frac{12}{7}$cm.
点评 本题考查的是相似三角形在实际生活中的应用,能根据题意画出图形,作出辅助线,再根据相似三角形的判定定理及性质进行解答.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{27}$ | B. | $\frac{6}{27}$ | C. | $\frac{1}{27}$ | D. | $\frac{8}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 品种A | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种B | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
| A品种作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| A品种作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.4 | 0.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com