
一个棱锥的三视图如图,则该棱锥的全面积(单位: )为
)为
A. | B. |
C. | D. |
A
解析试题分析:由三视图及题设条件知,此几何体为一个三棱锥,其高已知,底面是长度为6的直角三角形,故先求出底面积,再各个侧面积,最后相加即可得全面积
解:此几何体为一个三棱锥,其底面是边长为6的等腰直角三角形,顶点在底面的投影是斜边的中点,由底面是边长为6的等腰直角三角形知其底面积是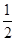 ×6×6=18
×6×6=18
又直角三角形斜边的中点到两直角边的距离都是3,棱锥高为4,
所以三个侧面中与底面垂直的侧面三角形高是4,底面边长为6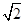 ,其余两个侧面的斜高为
,其余两个侧面的斜高为 =5故三个侧面中与底面垂直的三角形的面积为
=5故三个侧面中与底面垂直的三角形的面积为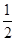 ×4×6
×4×6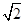 =12
=12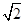 ,
,
另两个侧面三角形的面积都是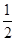 ×6×5=15
×6×5=15
故此几何体的全面积是18+2×15+12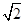 =48+12
=48+12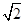
故选A
考点:三视图求几何体的面积、体积
点评:本题考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是三棱锥的体积.三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”.三视图是高考的新增考点,不时出现在高考试题中,应予以重视


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:单选题
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6则该球的表面积为
A.16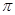 | B.24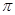 | C.32 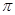 | D.48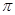 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图在棱长为5的正方体 中,
中, 是棱
是棱 上的一条线段,且
上的一条线段,且 ,
, 是
是 中点,点
中点,点 是棱
是棱 上动点,则四面体
上动点,则四面体 的体积( )
的体积( )
| A.是变量且有最大值 | B.是变量且有最小值 |
| C.是变量且有最大值和最小值 | D.是常量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com