
分析 (1)分N在抛物线内外两种情况讨论,根据抛物线的性质列方程得出p;
(2)设l方程为x=my+t,联立方程组得出A,B两点坐标与m,t的关系,代入两点间的距离公式化简即可得出结论.
解答 解:(1)①若N在抛物线内部,
则Q到抛物线C准线的距离与其到点N距离之和得最小值等于N到准线的距离,
∴$\frac{p}{2}$+7=10,解得p=6,不符合题意.
②若N在抛物线外部,则Q到抛物线C准线的距离与其到点N(7,8)距离之和的最小值等于|NF|.
∴$\sqrt{(7-\frac{p}{2})^{2}+{8}^{2}}$=10,解得p=2.
∴抛物线方程为y2=4x.
(2)设直线l的方程为x=my+t,
联立方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+t}\end{array}\right.$,得y2-4my-4t=0.
设A(x1,y1),B(x2,y2),∴y1+y2=4m,y1y2=-4t.
∴$\frac{1}{|AT{|}^{2}}$=$\frac{1}{({x}_{1}-t)^{2}+{{y}_{1}}^{2}}$=$\frac{1}{{m}^{2}{{y}_{1}}^{2}+{{y}_{1}}^{2}}$=$\frac{1}{(1+{m}^{2}){{y}_{1}}^{2}}$.
$\frac{1}{|BT{|}^{2}}$=$\frac{1}{({x}_{2}-t)^{2}+{{y}_{2}}^{2}}$=$\frac{1}{{m}^{2}{{y}_{2}}^{2}+{{y}_{2}}^{2}}$=$\frac{1}{(1+{m}^{2}){{y}_{2}}^{2}}$.
∴$\frac{1}{|AT{|}^{2}}+\frac{1}{|BT{|}^{2}}$=$\frac{1}{(1+{m}^{2}){{y}_{1}}^{2}}$+$\frac{1}{(1+{m}^{2}){{y}_{2}}^{2}}$=$\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}}{(1+{m}^{2}){{y}_{1}}^{2}{{y}_{2}}^{2}}$=$\frac{{m}^{2}+\frac{t}{2}}{(1+{m}^{2}){t}^{2}}$.
∴当$\frac{t}{2}$=1即t=2时,$\frac{1}{|AT{|}^{2}}+\frac{1}{|BT{|}^{2}}$=$\frac{1}{4}$.
∴存在实数t=2使得$\frac{1}{|AT{|}^{2}}+\frac{1}{|BT{|}^{2}}$为定值.
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ②③ | C. | ①② | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
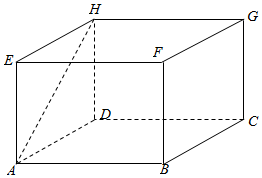 如图所示,长方体ABCD-EFGH,底面是边长为2$\sqrt{3}$的正方形,DH=2,P为AH中点.
如图所示,长方体ABCD-EFGH,底面是边长为2$\sqrt{3}$的正方形,DH=2,P为AH中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | ($\frac{1}{2}$,0) | C. | (1,0) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
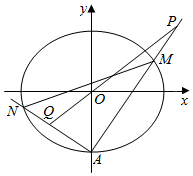 在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,连接椭圆C的四个顶点所形成的四边形面积为4$\sqrt{3}$.
在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,连接椭圆C的四个顶点所形成的四边形面积为4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com