
已知正方形ABCD的边长为1,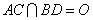 .将正方形ABCD沿对角线
.将正方形ABCD沿对角线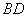 折起,使
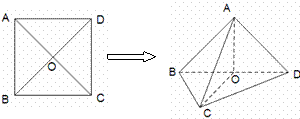
折起,使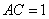 ,得到三棱锥A—BCD,如图所示.
,得到三棱锥A—BCD,如图所示.
(I)若点M是棱AB的中点,求证:OM∥平面ACD;
(II)求证: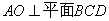 ;
;
 (III)求二面角
(III)求二面角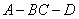 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
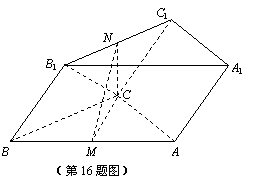
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB^平面CMN.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
将甲、乙、丙等六人分配到高中三个年级,每个年级2人,要求甲必须在高一年级,乙和丙均不能在高三年级,则不同的安排种数为
A.18 B.15 C.12 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com