
【题目】已知![]() 且
且![]() ,直线:
,直线: ![]() ,圆
,圆![]() :
:![]()
![]() .
.
(Ⅰ)若![]() ,请判断直线与圆
,请判断直线与圆![]() 的位置关系;
的位置关系;
(Ⅱ)求直线倾斜角![]() 的取值范围;
的取值范围;
(Ⅲ)直线能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
【答案】(1) 直线与圆![]() 相交;(2)
相交;(2) ![]() ;(3)直线不能将圆
;(3)直线不能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段弧.
的两段弧.
【解析】试题分析:(Ⅰ)若![]() ,求出圆心C(4,﹣2)到直线l的距离,与半径的关系,即可判断直线l与圆C的位置关系;
,求出圆心C(4,﹣2)到直线l的距离,与半径的关系,即可判断直线l与圆C的位置关系;
(Ⅱ)直线![]() ,可得:
,可得: ![]() ,利用均值不等式,即可得到直线倾斜角
,利用均值不等式,即可得到直线倾斜角![]() 的取值范围;
的取值范围;
(Ⅲ)判断![]() .若直线l能将圆C分割成弧长的比值为
.若直线l能将圆C分割成弧长的比值为![]() 的两段圆弧,则圆心C到直线l的距离
的两段圆弧,则圆心C到直线l的距离![]() ,即可得出结论.
,即可得出结论.
试题解析:
(Ⅰ)圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
若![]() ,直线:
,直线: ![]() ,即
,即![]() ,
,
则圆心![]() 到直线的距离
到直线的距离 ,
,
所以直线与圆![]() 相交.
相交.
(Ⅱ)直线的方程可化为![]() ,
,
直线的斜率![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
所以斜率的取值范围是![]() .
.
所以![]() 的范围为
的范围为![]()
(Ⅲ)能.由(Ⅰ)知直线恒过点![]() ,
,
设直线的方程为![]() ,其中
,其中![]() .
.
圆心![]() 到直线的距离
到直线的距离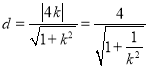 .
.
由![]() 得
得![]() ,又
,又![]() 即
即![]() .
.
若直线能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧,则圆心
的两段圆弧,则圆心![]() 到直线的距离
到直线的距离![]() ,
,
因为![]() ,所以直线不能将圆
,所以直线不能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段弧.
的两段弧.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】1979年,李政道博士给中国科技大学少年班出过一道智趣题:5只猴子分一堆桃子,怎么也不能分成5等份,只好先去睡觉,准备第二天再分,夜里1只猴子偷偷爬起来,先吃掉一个桃子,然后将其分成5等份,藏起自己的一份就去睡觉了;第2只猴子又爬起来,将剩余的桃子吃掉一个后,也将桃子分成5等份;藏起自己的一份睡觉去了;以后的3只猴子都先后照此办理,问:最初至少有多少个桃子?最后至少剩下多少个桃子?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx,sinωx),
=(cosωx,sinωx), ![]() =(cosωx,
=(cosωx, ![]() cosωx),其中ω>0,设函数f(x)=
cosωx),其中ω>0,设函数f(x)= ![]()
![]() .
.
(1)若函数f(x)的最小正周期是π,求函数f(x)的单调递增区间;
(2)若函数f(x)的图象的一个对称中心的横坐标为 ![]() ,求ω的最小值.
,求ω的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求![]() 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程![]() 是否有实数解 .
是否有实数解 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2≤5x﹣4的解集为A.
(1)求集合A;
(2)设关于x的不等式x2﹣(a+2)x+2a≤0的解集为M,若MA,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com