
【题目】设不等式x2≤5x﹣4的解集为A.
(1)求集合A;
(2)设关于x的不等式x2﹣(a+2)x+2a≤0的解集为M,若MA,求实数a的取值范围.
【答案】
(1)解:原不等式即为x2﹣5x+4=(x﹣1)(x﹣4)≤0,所以1≤x≤4所以不等式的解集A={x|1≤x≤4}
(2)解:不等式等价于(x﹣a)(x﹣2)≤0
若a<2,则M=[a,2],要MA,只需1≤a<2
若a>2,则M=[2,a],要MA,只需2<a≤4
若a=2,则M=2,符合MA(13分)
综上所述,a的取值范围为[1,4].
【解析】(1)求出不等式x2≤5x﹣4的解集确定出集合A,(2)若BA,求实数m的取值范围进要注意B是空集的情况,故此题分为两类求,是空集时,不是空集时,比较两个集合的端点即可.
【考点精析】通过灵活运用解一元二次不等式,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边即可以解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边即可以解答此题.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,直线:
,直线: ![]() ,圆
,圆![]() :
:![]()
![]() .
.
(Ⅰ)若![]() ,请判断直线与圆
,请判断直线与圆![]() 的位置关系;
的位置关系;
(Ⅱ)求直线倾斜角![]() 的取值范围;
的取值范围;
(Ⅲ)直线能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 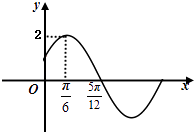
(1)求函数f(x)的解析式;
(2)令g(x)=f(﹣x﹣ ![]() ),求g(x)的单调递增区间.
),求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a2+bc=b2+c2
(1)求∠A的大小;
(2)若b=2,a= ![]() ,求边c的大小;
,求边c的大小;
(3)若a= ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() :
: ![]() 平分圆
平分圆![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点是
的两个焦点是![]() 和
和![]() ,并且经过点
,并且经过点![]() ,抛物线
,抛物线![]() 的顶点在坐标原点,焦点恰好是椭圆
的顶点在坐标原点,焦点恰好是椭圆![]() 的右顶点.
的右顶点.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() 为抛物线
为抛物线![]() 内一个定点,过
内一个定点,过![]() 作斜率分别为
作斜率分别为![]() 的两条直线交抛物线
的两条直线交抛物线![]() 于点
于点![]() ,且
,且![]() 分别是
分别是![]() 的中点,若
的中点,若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com