练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的两个焦点是和，并且经过点，抛物线的顶点在坐标原点，焦点恰好是椭圆的右顶点.

    （Ⅰ）求椭圆和抛物线的标准方程；

    （Ⅱ）已知点为抛物线内一个定点，过作斜率分别为的两条直线交抛物线于点，且分别是的中点，若，求证：直线过定点.

    【答案】（1）；（2）.

    【解析】试题分析：（1）根据椭圆的定义，可以求出，再根据求出即可写出椭圆方程及抛物线方程；（2）设直线AB方程，联立抛物线方程化简，由根与系数的关系易得M的坐标，同理可得N的坐标，写出MN直线方程，可以看出直线过定点.

    试题解析：（1）设椭圆的标准方程为，焦距是，则由题意得：

    ， ，∴，椭圆的标准方程为： .

    ∴右顶点的坐标为，设抛物线的标准方程为： ，∴，∴抛物线的标准方程为： .

    （2） ，由得

    ，则，所以，同理

    ∴，则，即

    其恒过定点

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设不等式x2≤5x﹣4的解集为A．
    （1）求集合A；
    （2）设关于x的不等式x2﹣（a+2）x+2a≤0的解集为M，若MA，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： ，与轴不重合的直线经过左焦点，且与椭圆相交于， 两点，弦的中点为，直线与椭圆相交于， 两点．

    （Ⅰ）若直线的斜率为1，求直线的斜率；

    （Ⅱ）是否存在直线，使得成立？若存在，求出直线的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|ax+1|+|2x﹣1|（a∈R）．

    （1）当a=1时，求不等式f（x）≥2的解集；

    （2）若f（x）≤2x在x∈[，1]时恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，甲船以每小时 海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于A1处时，乙船位于甲船的北偏西105°方向的B1处，此时两船相距20海里，当甲船航行20分钟到达A2处时，乙船航行到甲船的北偏西120°方向的B2处，此时两船相距 海里，问乙船每小时航行多少海里？

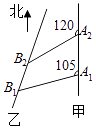
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以下关于命题的说法正确的有（选择所有正确命题的序号）.

    （1）“若，则函数在其定义域内是减函数”是真命题；

    （2）命题“若，则”的否命题是“若，则”；

    （3）命题“若都是偶函数，则也是偶数”的逆命题为真命题；

    （4）命题“若，则”与命题“若，则”等价.

    A. （1）（3） B. （2）（3） C. （2）（4） D. （3）（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 且cos（ ）= ，sin 求cos（α+β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足log3an+1=log3an+1（n∈N*），且a2+a4+a6=9，则log （a5+a7+a9）的值是（ ）
    A.﹣
    B.﹣5
    C.5
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A,B,C的坐标分别为A(3,0),B(0,3),C(cos α,sin α),α∈.

    (1)若||=||,求角α的值;

    (2)若=-1,求的值.

    查看答案和解析>>

    同步练习册答案