
【题目】已知如图,椭圆![]() :
:![]() 与直线
与直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.

(Ⅰ)若直线![]() 经过椭圆
经过椭圆![]() 的左焦点
的左焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() ,
,![]() .求证:
.求证:![]() 为定值;
为定值;
(Ⅱ)若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)设出直线方程,设出AB的坐标,直线方程代入椭圆方程,利用韦达定理结合![]() ,
,![]() .即可证明:λ+μ为定值;(Ⅱ)当直线OA,OB分别与坐标轴重合时,易知
.即可证明:λ+μ为定值;(Ⅱ)当直线OA,OB分别与坐标轴重合时,易知![]() .当直线OA,OB斜率存在且不为0时,设
.当直线OA,OB斜率存在且不为0时,设![]() ,设
,设![]() ,
,![]() ,直线y=kx代入椭圆C得到x2+2k2x2﹣2=0,求出A,B坐标,表示出三角形的面积,利用换元法转化为二次函数求解三角形的面积的范围.
,直线y=kx代入椭圆C得到x2+2k2x2﹣2=0,求出A,B坐标,表示出三角形的面积,利用换元法转化为二次函数求解三角形的面积的范围.
(Ⅰ)证明:由题设知直线![]() 斜率存在,设直线
斜率存在,设直线![]() 方程为
方程为![]() ,则
,则![]() .
.
设![]() ,
,![]() ,直线
,直线![]() 代入椭圆
代入椭圆![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,
,![]() 知
知![]() ,
,![]() ,
,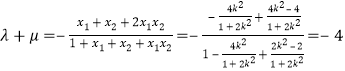 .
.
(Ⅱ)当直线![]() ,
,![]() 分别与坐标轴重合时,易知
分别与坐标轴重合时,易知![]() .
.
当直线![]() ,
,![]() 斜率存在且不为0时,设
斜率存在且不为0时,设![]() :
:![]() ,
,![]() :
:![]() ,
,
设![]() ,
,![]() ,直线
,直线![]() 代入椭圆
代入椭圆![]() 得到
得到![]() ,
,
所以![]() ,
,![]() ,
,
同理![]() ,
,![]() ,
,
![]()
![]() ,
,
令![]() ,
,
则![]()
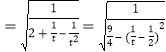 ,
,
因为![]() ,所以
,所以![]() ,
,
故![]() ,综上
,综上![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两城相距100![]() ,在两城之间距甲城
,在两城之间距甲城![]()
![]() 处的丙地建一核电站给甲、乙两城供电,为保证城市安全,核电站距两地的距离不少于10
处的丙地建一核电站给甲、乙两城供电,为保证城市安全,核电站距两地的距离不少于10![]() .已知各城供电费用(元)与供电距离(
.已知各城供电费用(元)与供电距离(![]() )的平方和供电量(亿千瓦时)之积都成正比,比例系数均是
)的平方和供电量(亿千瓦时)之积都成正比,比例系数均是![]() =0.25,若甲城供电量为20亿千瓦时/月,乙城供电量为10亿千瓦时/月,
=0.25,若甲城供电量为20亿千瓦时/月,乙城供电量为10亿千瓦时/月,
(1)把月供电总费用![]() (元)表示成
(元)表示成![]() (
(![]() )的函数,并求其定义域;
)的函数,并求其定义域;
(2)求核电站建在距甲城多远处,才能使月供电总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在塔的正东方向沿着南偏西60°的方向前进40 m以后,望见塔在东北方向上,若沿途测得塔的最大仰角为30°,则塔高为________________m.
查看答案和解析>>
科目:高中数学 来源: 题型:
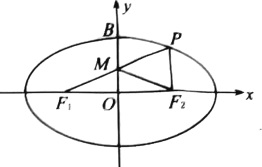
【题目】如图,已知![]() ,
, ![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点, ![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线分别与椭圆
作两条互相垂直的直线分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点(异于点
两点(异于点![]() ),证明:直线
),证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B,C,D四所中学报名参加某高校2015年自主招生考试的学生人数如下表所示:
中学 | A | B | C | D |
人数 | 40 | 30 | 10 | 20 |
该市教委为了解参加考试的学生的学习状况,采用分层抽样的方法从四所中学报名参加考试的学生中随机抽取50名参加问卷调查.则A,B,C,D四所中学抽取的学生人数分别为( )
A.15,20,10,5B.15,20,5,10
C.20,15,10,5D.20,15,5,10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出2个小球,每个小球被取出的可能性相等.
(1)求从甲盒中取出的两个球上的编号不都是奇数的概率;
(2)求从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
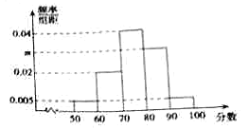
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300千米的海面
方向300千米的海面![]() 处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com