
分析 由已知及等差数列的性质可得A+C=3B,结合三角形内角和定理可求B的值,利用三角形面积公式可得$ac=2(2+\sqrt{2})$,利用余弦定理及基本不等式即可解得AC边的最小值.
解答 解:∵A、$\frac{3}{2}$B、C成等差数列,
∴A+C=3B,
又∵A+B+C=π,
∴$B=\frac{π}{4}$,
∴由${S_{△ABC}}=\frac{1}{2}acsinB=1+\sqrt{2}$得$ac=2(2+\sqrt{2})$,
∵b2=a2+c2-2accosB=${a^2}+{c^2}-\sqrt{2}ac$,及a2+c2≥2ac,
∴${b^2}≥(2-\sqrt{2})ac=4$,解得:b≥2,
∴b的最小值为2.
故答案为:2.
点评 本题主要考查了等差数列的性质,三角形内角和定理,三角形面积公式,余弦定理,基本不等式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | a | b | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
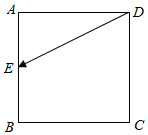 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{2}{3}$,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆或椭圆 | B. | 抛物线或双曲线 | C. | 椭圆或双曲线 | D. | 以上都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com