Question

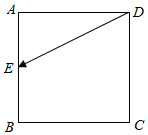
3．如图所示，已知正方形ABCD的边长为1，点E从D点出发，按字母顺序D→A→B→C沿线段DA，AB，BC运动到C点，在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是（　　）

• A． 0
• B． $\frac{1}{2}$
• C． 1
• D． -1

Answer 1

分析 建系，由向量数量积的坐标运算公式，分类讨论，结合点E的运动，即可求出最大值．

解答 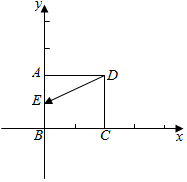解：以BC、BA所在直线为x轴、y轴，建立坐标系如图
可得A（0，1），B（0，0），C（1，0），D（1，1），
当E在DA上，设E（x，1），其中0≤x≤1
∵$\overrightarrow{DE}$=（x-1，0），$\overrightarrow{CD}$=（0，1），
∴$\overrightarrow{DE}•\overrightarrow{CD}$=0，
当E在AB上，设E（0，y），其中0≤y≤1
∵$\overrightarrow{DE}$=（-1，y-1），$\overrightarrow{CD}$=（0，1），
∴$\overrightarrow{DE}•\overrightarrow{CD}$=y-1，（0≤y≤1），此时最大值为0，
当E在BC上，设E（x，0），其中0≤x≤1
∵$\overrightarrow{DE}$=（x-1，-1），$\overrightarrow{CD}$=（0，1），
∴$\overrightarrow{DE}•\overrightarrow{CD}$=-1，
当E在CD上，设E（1，y），其中0≤y≤1
∵$\overrightarrow{DE}$=（0，y-1），$\overrightarrow{CD}$=（0，1），
∴$\overrightarrow{DE}•\overrightarrow{CD}$=y-1，（0≤y≤1），此时最大值为0，
综上所述$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是0，
故选：A．

点评 本题考查向量数量积的最大值，建立坐标系是解决问题的关键，属中档题．