
分析 由二次函数的性质可得二次函数f(x)=3ax2-2(a+b)x+b的图象开口向上,且其对称轴为x=$\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$,从而可得|1-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|≥|0-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|,从而解得.
解答 解:∵f(x)=3ax2-2(a+b)x+b,
∴f(1)=3a-2(a+b)+b=a-b,
又∵函数f(x)的最大值是a-b,
函数f(x)=3ax2-2(a+b)x+b在x=1处取得最大值,
又∵a>0,
∴二次函数f(x)=3ax2-2(a+b)x+b的图象开口向上,
且其对称轴为x=$\frac{a+b}{3a}$=$\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$,
∴|1-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|≥|0-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|,
即$\frac{b}{a}$≤$\frac{1}{2}$.
点评 本题考查了二次函数的性质的判断与应用,同时考查了数形结合的思想应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{22}{81}$ | B. | $\frac{7}{12}$ | C. | $\frac{11}{18}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 职称类型 | 相关人数 | 抽取人数 |
| 初级 | 27 | x |
| 中级 | 99 | y |
| 高级 | 18 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
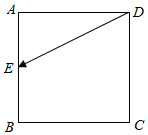 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{2}{3}$,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,x2<0 | B. | ?x≤0,x2≥0 | C. | ?x0>0,x02>0 | D. | ?x0<0,x02≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com