
已知直线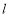 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆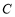 的极坐标方程为
的极坐标方程为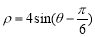 .求:
.求:
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)若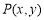 是直线
是直线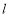 与圆面
与圆面 ≤
≤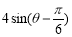 的公共点,求
的公共点,求 的取值范围.
的取值范围.
(1)
 .(2)
.(2)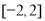 .
.
【解析】
试题分析:(1)先将 利用两角差的正弦公式展开,方程两边在乘以
利用两角差的正弦公式展开,方程两边在乘以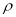 ,利用直角坐标与极坐标互化公式即可将极坐标方程互为直角坐标方程;(2)先将直线方程化为普通方程互化,求出直线与圆的交点A、B坐标,作出直线
,利用直角坐标与极坐标互化公式即可将极坐标方程互为直角坐标方程;(2)先将直线方程化为普通方程互化,求出直线与圆的交点A、B坐标,作出直线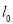 :
: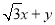 =0,平移直线
=0,平移直线 ,结合图形,找出直线z=
,结合图形,找出直线z=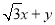 与线段AB相交时,z取最大值与最小值点,求出z的最大值与最小值,即可求出
与线段AB相交时,z取最大值与最小值点,求出z的最大值与最小值,即可求出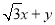 的取值范围.
的取值范围.
试题解析:(1)因为圆 的极坐标方程为
的极坐标方程为
所以
又
所以
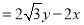
所以圆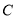 的直角坐标方程为:
的直角坐标方程为:
 . 6分
. 6分
(2)『解法1』:
设
由圆 的方程
的方程

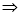
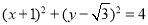
所以圆 的圆心是
的圆心是 ,半径是
,半径是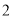
将 代入
代入 得
得
又直线 过
过 ,圆
,圆 的半径是
的半径是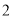 ,由题意有:
,由题意有: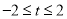
所以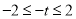
即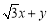 的取值范围是
的取值范围是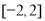 . 14分
. 14分
『解法2』:
直线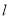 的参数方程化成普通方程为:
的参数方程化成普通方程为:
由
解得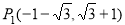 ,
,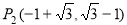
∵ 是直线
是直线 与圆面
与圆面 的公共点,
的公共点,
∴点 在线段
在线段 上,
上,
∴ 的最大值是
的最大值是 ,
,
最小值是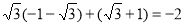
∴ 的取值范围是
的取值范围是 . 14分
. 14分
考点:极坐标方程与直角坐标方程互化;参数方程与普通方程互化互化;直线与圆的位置关系;数形结合想


科目:高中数学 来源:2015届山西省忻州市高二下学期期中联考文科数学试卷(解析版) 题型:选择题
给出下列四个命题:
① 因为 ,所以
,所以 ;
;
② 由 两边同除
两边同除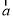 ,可得
,可得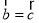 ;
;
③ 数列1,4,7,10,…,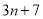 的一个通项公式是
的一个通项公式是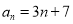 ;
;
④ 演绎推理是由一般到特殊的推理,类比推理是由特殊到特殊的推理.
其中正确命题的个数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设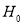 :“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出
:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出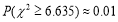 ,则下列说法正确的( )
,则下列说法正确的( )
A.这种疫苗能起到预防甲型H1N1流感的有效率为1%
B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1
C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考理科数学试卷(解析版) 题型:选择题
若函数f(x)=2x2 lnx在其定义域的一个子区间(k 1,k+1)上不是单调函数,则实数k的取值范围是( )
A. ( ,+ ?) B. ( ?,
,+ ?) B. ( ?,  ) C. (
) C. ( ,
, ) D. [1,
) D. [1,  )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com