Question

18．在平行四边形ABCD中O是对角线交点，E是OD中点，连接AE交CD于F，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，则用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AF}$=$-\frac{4}{3}\overrightarrow{a}-\frac{2}{3}\overrightarrow{b}$．

Answer 1

分析 根据条件便可得出$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AD}+\frac{1}{4}\overrightarrow{AC}$，而由A，E，F共线便可设$\overrightarrow{AF}=k\overrightarrow{AE}=\frac{k}{2}\overrightarrow{AD}+\frac{k}{4}\overrightarrow{AC}$，而由D，F，C三点共线便可得出$\frac{k}{2}+\frac{k}{4}=1$，从而求得$k=\frac{4}{3}$，这样便可得到$\overrightarrow{AF}=\frac{2}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{AO}$．而容易用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{AD}，\overrightarrow{AO}$，从而便可用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{AF}$．

解答 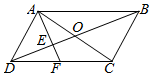解：如图，根据条件：
$\overrightarrow{AD}=-（\overrightarrow{DO}+\overrightarrow{OA}）=-（\overrightarrow{b}+\overrightarrow{a}）$，$\overrightarrow{AO}=-\overrightarrow{a}$；
∵E是OD中点，O是AC中点；
∴$\overrightarrow{AE}=\frac{1}{2}（\overrightarrow{AD}+\overrightarrow{AO}）$=$\frac{1}{2}（\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AC}）$=$\frac{1}{2}\overrightarrow{AD}+\frac{1}{4}\overrightarrow{AC}$；
∵A，E，F三点共线，设$\overrightarrow{AF}=k\overrightarrow{AE}$=$\frac{k}{2}\overrightarrow{AD}+\frac{k}{4}\overrightarrow{AC}$；
又D，F，C三点共线；
∴$\frac{k}{2}+\frac{k}{4}=1$；
∴$k=\frac{4}{3}$；
∴$\overrightarrow{AF}=\frac{4}{3}\overrightarrow{AE}=\frac{4}{3}•\frac{1}{2}（\overrightarrow{AD}+\overrightarrow{AO}）$=$\frac{2}{3}（-\overrightarrow{b}-\overrightarrow{a}-\overrightarrow{a}）=-\frac{4}{3}\overrightarrow{a}-\frac{2}{3}\overrightarrow{b}$；
即$\overrightarrow{AF}=-\frac{4}{3}\overrightarrow{a}-\frac{2}{3}\overrightarrow{b}$．
故答案为：$-\frac{4}{3}\overrightarrow{a}-\frac{2}{3}\overrightarrow{b}$．

点评 考查向量加法的平行四边形法则，向量数乘的几何意义，以及向量的数乘运算，A，B，C三点共线的充要条件：$\overrightarrow{OB}=x\overrightarrow{OA}+y\overrightarrow{OB}$，且x+y=1，以及向量加法的几何意义．