
分析 由2x>0,求得2x+3的范围,取倒数求得$\frac{1}{{2}^{x}+3}$的范围,两边同时乘以-1,得到$-\frac{1}{{2}^{x}+3}$的范围,进一步求得函数的值域.
解答 解:f(x)=$\frac{{2}^{x}-3}{{2}^{x}+3}$=$\frac{{2}^{x}+3-6}{{2}^{x}+3}=1-\frac{6}{{2}^{x}+3}$,
∵2x>0,
∴2x+3>3,
则0$<\frac{1}{{2}^{x}+3}<\frac{1}{3}$,
∴$-\frac{1}{3}<-\frac{1}{{2}^{x}+3}<0$,
则-2$<-\frac{6}{{2}^{x}+3}<0$,
∴f(x)∈(-1,1).
故答案为:(-1,1).
点评 本题考查函数的值域,体现了极限思想方法的运用,是中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
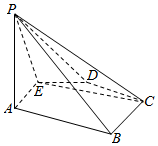 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com