已知函数f(x)是R上的偶函数.若对于x≥0.都有f.且当x∈[0.2)时.f(x)=log2+fA．-2B．-1C．1D．2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

1．已知函数f（x）是R上的偶函数，若对于x≥0，都有f（x+2）=f（x），且当x∈[0，2）时，f（x）=log₂（x+1），则f（-2014）+f（2015）的值为（　　）

A．

-2

B．

-1

C．

D．

分析由函数的性质可得f（-2014）+f（2015）=f（0）+f（1）=log₂（1+0）+log₂（1+1），计算对数可得．

解答解：∵函数f（x）是R上的偶函数，
∴f（-2014）=f（2014），
又∵对于x≥0，都有f（x+2）=f（x），
∴f（-2014）+f（2015）=f（2014）+f（2015）
=f（0）+f（1）=log₂（1+0）+log₂（1+1）=0+1=1
故选：C

点评本题考查函数的周期性和奇偶性，涉及对数函数的运算，属基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

11．

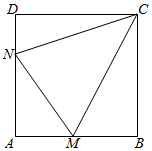如图所示，某村积极开展“美丽乡村•生态家园”建设，现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园，给村民休闲健身提供去处．点M，N分别在边AB，AD上．
（Ⅰ）当点M，N分别是边AB，AD的中点时，求∠MCN的余弦值；
（Ⅱ）由于村建规划及保护生态环境的需要，要求△AMN的周长为2千米，请探究∠MCN是否为定值，若是，求出此定值，若不是，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．若虚数z=（a-1）+ai（a∈R）的模为1，则a=1．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

为检验寒假学生自主学生的效果，级部对某班50名学生各科的检测成绩进行了统计，下面是物理成绩的频率分布直方图，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求图中的x值及平均成绩；
（2）从分数在[70，80）中选5人记为a₁，a₂，…，a₅，从分数在[40，50）中选3人，记为b₁，b₂，b₃，8人组成一个学习小组现从这5人和3人中各选1人做为组长，求a₁被选中且b₁未被选中的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

16．已知$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$是同一平面内的三个向量，其中$\overrightarrow{a}$，$\overrightarrow{b}$是相互垂直的单位向量，且（$\overrightarrow{a}-\overrightarrow{c}$）•（$\sqrt{3}\overrightarrow{b}$-$\overrightarrow{c}$）=1，|$\overrightarrow{c}$|的最大值为1+$\sqrt{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．设函数f（x）=$\sqrt{3}$sinxcosx+cos²x+a．
（1）当x∈[-$\frac{π}{6}$，$\frac{π}{3}$]时，函数f（x）的最大值与最小值的和为$\frac{3}{2}$．求f（x）的单调区间与对称中心
（2）当a=-$\frac{1}{2}$时，求出最小正实数m，使得函数f（x）的图象向右平移m个单位长度后所对应的函数是偶函数．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．已知点A（1，1），点P在曲线f（x）=x³-3x²+3x（0≤x≤2）上，点Q在直线y=3x-14上，M为线段PQ的中点，则|AM|的最小值为（　　）

A．

$\frac{2\sqrt{10}}{5}$

B．

$\frac{\sqrt{10}}{2}$

C．

$\sqrt{10}$

D．

$\frac{7\sqrt{10}}{5}$

查看答案和解析>>