
分析 (1)直接由等差数列的前n项和公式求数列{an}的前n项和Sn;
(2)由$\frac{1}{{S}_{n}}=\frac{1}{{n}^{2}+2n}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用裂项相消法求$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$.
解答 解:(1)∵数列{an}是等差数列,首项为3,公差为2,
∴${S}_{n}=n{a}_{1}+\frac{n(n-1)d}{2}=3n+\frac{2n(n-1)}{2}={n}^{2}+2n$,
(2)∵$\frac{1}{{S}_{n}}=\frac{1}{{n}^{2}+2n}=\frac{1}{n(n+2)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n}-\frac{1}{n+2})$
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{3}{4}-\frac{2n+3}{2(n+1)(n+2)}$.
点评 本题考查等差数列的前n项和,训练了裂项相消法求数列的和,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
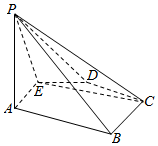 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
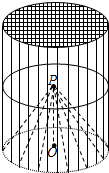 某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.
某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com