练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知复数z满足|z|=2，且ω=z2-z+4，试求|ω|的最值及取得最值时的复数z．

    分析 ω=z2-z+4=$（z-\frac{1}{2}）^{2}$+$\frac{15}{4}$，点P$（\frac{1}{2}，0）$在圆|z|=2内，并且到原点O的距离d=$\frac{1}{2}$，即可得出．

    解答 解：ω=z2-z+4=$（z-\frac{1}{2}）^{2}$+$\frac{15}{4}$，
    点P$（\frac{1}{2}，0）$在圆|z|=2内，并且到原点O的距离d=$\frac{1}{2}$，
    ∴当z=2时，|ω|取得最小值6；
    当z=-2时，|ω|取得最大值10．

    点评 本题考查了复数模的计算公式、圆的复数形式的方程、复数的几何意义，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．为检验寒假学生自主学生的效果，级部对某班50名学生各科的检测成绩进行了统计，下面是物理成绩的频率分布直方图，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
    （1）求图中的x值及平均成绩；
    （2）从分数在[70，80）中选5人记为a1，a2，…，a5，从分数在[40，50）中选3人，记为b1，b2，b3，8人组成一个学习小组现从这5人和3人中各选1人做为组长，求a1被选中且b1未被选中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．函数f（x）=$\frac{{2}^{x}-3}{{2}^{x}+3}$的值域为（-1，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若二项式（ax-$\frac{1}{x}$）6展开式中各项系数之和为1，则x4的系数为-192．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若a1=3，a2=6，且an+2=an+1-an，则a2016等于-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若函数f（x）=2sin（ωx-$\frac{π}{3}$）（ω＞0）的图象两相邻对称轴之间的距离为3，则f（0）+f（1）+f（2）+…+f（2016）=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知数列{an}是等差数列，首项为3，公差为2．
    （1）求数列{an}的前n项和Sn；
    （2）求和：$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{n}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知正方形ABCD的边长为1，点E，F分别为BC、CD的中点，则$\overrightarrow{AE}$•$\overrightarrow{BD}$=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

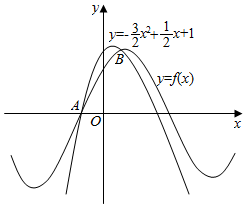    9．如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A（x1，0）和B（x2，1），则f（x）的解析式为（　　）
    A．f（x）=sin（$\frac{1}{6}$x+$\frac{π}{3}$）B．f（x）=sin（$\frac{1}{2}$x+$\frac{π}{3}$）C．f（x）=sin（$\frac{π}{2}$x+$\frac{π}{3}$）D．f（x）=sin（$\frac{π}{2}$x+$\frac{π}{6}$）

    查看答案和解析>>

    同步练习册答案