
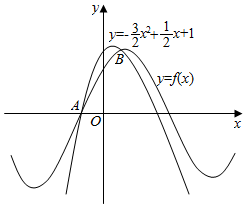
 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )| A. | f(x)=sin($\frac{1}{6}$x+$\frac{π}{3}$) | B. | f(x)=sin($\frac{1}{2}$x+$\frac{π}{3}$) | C. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$) | D. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{6}$) |
分析 利用二次函数求出A,B两点的坐标,根据正弦函数的性质得出f(x)的周期,代入特殊点B的坐标即可求出φ.
解答 解:把y=0代入二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1得x=1或x=-$\frac{2}{3}$.
由图象可知x1<0,∴A(-$\frac{2}{3}$,0).
把y=1代入二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1得x=0或x=$\frac{1}{3}$.
由图象可得x2>0,∴B($\frac{1}{3}$,1).
∴f(x)的周期T=$\frac{2π}{ω}=4×(\frac{1}{3}+\frac{2}{3})$=4,解得ω=$\frac{π}{2}$.
把B($\frac{1}{3}$,1)代入f(x)得sin($\frac{π}{6}$+φ)=1,∴$\frac{π}{6}+$φ=$\frac{π}{2}+$2kπ,
∴φ=$\frac{π}{3}$+2kπ,k∈Z.∵|φ|$<\frac{π}{2}$,∴φ=$\frac{π}{3}$.
∴f(x)=sin($\frac{π}{2}x+\frac{π}{3}$).
故选:C.
点评 本题考查了y=Asin(ωx+φ)的函数图象与性质,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
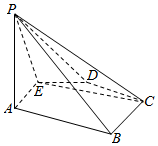 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | ($\overrightarrow{a}•\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}•\overrightarrow{c}$) | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}•\overrightarrow{c}$+$\overrightarrow{b}•\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
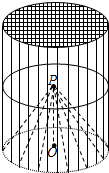 某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.
某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b>0,则$\frac{b}{a}$>$\frac{b+1}{a+1}$ | B. | 若a>b>0,则lg$\frac{a+b}{2}$<$\frac{lga+lgb}{2}$ | ||
| C. | 若a>b>0,则a+$\frac{1}{b}$>b+$\frac{1}{a}$ | D. | 若a>b>0,则$\sqrt{a}-\sqrt{b}$>$\sqrt{a-b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com