
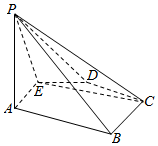
 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.分析 (1)欲证明BC∥平面PAE,只需推知BC∥AE即可;
(2)只需推知CF⊥平面PAE,即可证得PA⊥FC.
解答 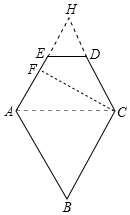 证明:(1)如图,凸五边形ABCDE,延长AE、CD交于点H.
证明:(1)如图,凸五边形ABCDE,延长AE、CD交于点H.
∵∠AED=∠EDC=120°,
∴∠HED=∠HDE=60°,∴△HED为等边三角形,
∠H=60°.
∴∠H+∠BCD=60°+120°=180°,
∴BC∥AE.
又∵AE?平面PAE,BC?平面PAE,
∴BC∥平面PAE;
(2)如图,连结AC.
∵△HED是等边三角形,
∴HE=HD=ED=1,
∴HC=HA=3.
又∵∠H=60°,
∴△HAC为等边三角形.
又∵AF=$\frac{1}{2}$AH,
∴CF⊥AE.
∵平面PAE⊥平面ABCDE,平面PAE∩平面ABCDE=AE,CF?平面ABCDE,
∴CF⊥平面PAE.
又∵PA?平面PAE,
∴PA⊥FC.
点评 本题考查直线与平面垂直的判定,直线与平面所成的角的求法,考查学生空间想象能力,逻辑思维能力,是中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大量的试验中,出现正面的频率稳定于$\frac{1}{2}$ | |
| B. | 不管试验多少次,出现正面的概率始终为$\frac{1}{2}$ | |
| C. | 试验次数增多,出现正面的经验概率越接近$\frac{1}{2}$ | |
| D. | 试验次数无限增大时,出现正面的频率的极限为$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
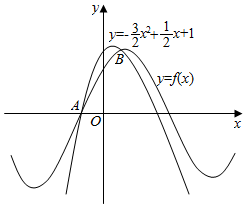 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )| A. | f(x)=sin($\frac{1}{6}$x+$\frac{π}{3}$) | B. | f(x)=sin($\frac{1}{2}$x+$\frac{π}{3}$) | C. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$) | D. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
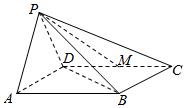 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com