
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用复合命题的真假判断①的正误;命题的否定判断②的正误;充要条件判断③的正误.二项式定理判断④的正误.
解答 解:①若“命题p∧q为真”,则p,q都为真命题,所以“命题p∨q为真”,故正确;
②命题“?x>0,x-lnx>0”的否定是“?x>0,x-lnx≤0”,满足命题的否定形式,正确;
③“tanx>0”可得x∈(kπ,kπ+$\frac{π}{2}$),k∈Z;“sin2x>0“可得2x∈(2kπ,2kπ+π),即x∈(kπ,kπ+$\frac{π}{2}$),k∈Z;所以“tanx>0”是“sin2x>0“的充要条件.正确;
④由于9192=(100-9)92=C920•10092•(-9)0+…+C9291•1001•(-9)91+C9292•1000•(-9)92,
在此展开式中,除了最后一项外,其余的项都能被100整除,故9192除以100的余数等价于C9292•1000•(-9)92=992除以100的余数,而992=(10-1)92=C920•1092•(-1)0+…+C9291•101•(-1)91+C9292•100•(-9)92,故992除以100的余数等价于C9291•101•(-1)91+C9292•100•(-9)92除以100的余数,而C9291•101•(-1)91+C9292•100•(-9)92=-919=-10×100+81,故9192除以100的余数是81.不正确.
故选:C.
点评 本题考查命题的真假的判断与应用,考查充要条件,命题的否定,二项式定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
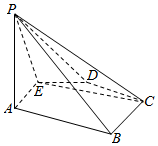 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | ($\overrightarrow{a}•\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}•\overrightarrow{c}$) | D. | ($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{c}$=$\overrightarrow{a}•\overrightarrow{c}$+$\overrightarrow{b}•\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
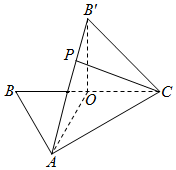 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2,将△BAO沿AO折起,使B点到达B′点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com