
分析 (1)求出抛物线的焦点,设A(x1,y1),B(x2,y2),D(x3,y3),运用重心坐标公式,可得x1+x2+x3=2e,y1+y2+y3=0,由题意可得一点在x轴上,且与原点重合,另外两点的连线垂直于x轴,可得m=e,即有k≥-e,先求出x1,x2的范围,令H(x)=lnx1+lnx2,运用构造函数法,通过判断函数的单调性证出结论即可得到所求范围;
(2)不妨令x1<x2,得:0<x1<$\frac{1}{e}$<x2,构造F(x)=f($\frac{1}{e}$+x)-f($\frac{1}{e}$-x),x∈[0,$\frac{1}{e}$),求出函数的导数,得到f(x2)>f($\frac{2}{e}$-x1)?x2>$\frac{2}{e}$-x1,从而得到结论.
解答 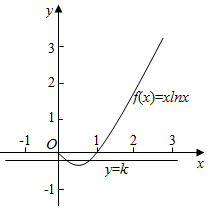 解:(1)抛物线${y}^{2}=\frac{8e}{3}x$的焦点为($\frac{2e}{3}$,0),
解:(1)抛物线${y}^{2}=\frac{8e}{3}x$的焦点为($\frac{2e}{3}$,0),
设A(x1,y1),B(x2,y2),D(x3,y3),
由题意可得x1+x2+x3=2e,y1+y2+y3=0,
当三角形ABD面积为最大时,三角形的三条边与x轴交于两点,
即有一点在x轴上,且与原点重合,另外两点的连线垂直于x轴,
可得m=e,即有k≥-e,
f(x)的定义域是(0,+∞),f′(x)=lnx+1,
令f′(x)>0,解得:x>$\frac{1}{e}$,令f′(x)<0,解得:0<x<$\frac{1}{e}$
∴f(x)在(0,$\frac{1}{e}$)递减,在($\frac{1}{e}$,+∞)递增,
∴f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$,f(1)=0,
画出函数f(x)的图象,如图示
可得-$\frac{1}{e}$<k<0,
x1lnx1=x2lnx2,设x1<x2,
则0<x1<$\frac{1}{e}$,x2>$\frac{1}{e}$,
令H(x)=lnx1+lnx2=lnx1+$\frac{{x}_{1}}{{x}_{2}}$lnx1=(1+$\frac{{x}_{1}}{{x}_{2}}$)lnx1,
∵x2>$\frac{1}{e}$,∴$\frac{{x}_{1}}{{x}_{2}}$<ex1,
∴H(x)<(1+ex1)lnx1,
令g(x)=(1+ex)lnx,(0<x<$\frac{1}{e}$),
则g′(x)=elnx+e+$\frac{1}{x}$,g″(x)=$\frac{ex-1}{{x}^{2}}$,
∵x<$\frac{1}{e}$,∴ex-1<0,
∴g″(x)<0,g′(x)是减函数,
又g′($\frac{1}{e}$)=e,∴g′(x)>g′($\frac{1}{e}$),g′(x)>0,
∴g(x)是增函数,又g($\frac{1}{e}$)=-2,
∴g(x)<g($\frac{1}{e}$)=-2,
∴H(x)<-2,
∴0<x1x2<$\frac{1}{{e}^{2}}$;
(2)由(1),不妨令x1<x2,得:0<x1<$\frac{1}{e}$<x2,
构造F(x)=f($\frac{1}{e}$+x)-f($\frac{1}{e}$-x),x∈[0,$\frac{1}{e}$),
F′(x)=ln($\frac{1}{e}$+x)+ln($\frac{1}{e}$-x)+2,
F″(x)=$\frac{2x}{{x}^{2}-\frac{1}{{e}^{2}}}$≤0恒成立,
F′(x)在x∈[0,$\frac{1}{e}$)上单调递减,
F′(x)≤F′(0)=0,F(x)在x∈[0,$\frac{1}{e}$)上单调递减,
F(x)≤F(0)=0,当且仅当x=0取“=”,
即对于x∈(0,$\frac{1}{e}$),f($\frac{1}{e}$+x)<f($\frac{1}{e}$-x)恒成立,
又0<x1<$\frac{1}{e}$,0<$\frac{1}{e}$-x1<$\frac{1}{e}$,
∴f(x2)=f(x1)=f[$\frac{1}{e}$-($\frac{1}{e}$-x1)]>f[$\frac{1}{e}$+($\frac{1}{e}$-x1)]
=f($\frac{2}{e}$-x1),
此时:$\frac{1}{e}$<x2,$\frac{1}{e}$<$\frac{2}{e}$-x1<$\frac{2}{e}$,
由f(x)的递增区间为($\frac{1}{e}$,+∞)知:
f(x2)>f($\frac{2}{e}$-x1)?x2>$\frac{2}{e}$-x1,
即x1+x2>$\frac{2}{e}$.
即有x1+x2的取值范围是($\frac{2}{e}$,1+$\frac{1}{e}$).
点评 本题考查抛物线的方程和性质,主要考查导数的运用:求单调区间、极值和最值,注意运用函数的单调性,考查不等式的性质,以及转化思想,是难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{10}$ | D. | $\frac{7\sqrt{10}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
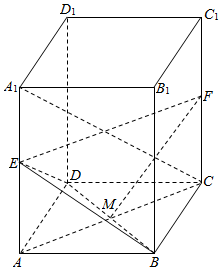 如图正四棱住ABCD-A1B1C1D1中,点E是A1A上的点,M是AC、BD的交点.
如图正四棱住ABCD-A1B1C1D1中,点E是A1A上的点,M是AC、BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大量的试验中,出现正面的频率稳定于$\frac{1}{2}$ | |
| B. | 不管试验多少次,出现正面的概率始终为$\frac{1}{2}$ | |
| C. | 试验次数增多,出现正面的经验概率越接近$\frac{1}{2}$ | |
| D. | 试验次数无限增大时,出现正面的频率的极限为$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com