
���� ��1�������Ǻ�����ʽ����ɵ�f��x��=sin��2x+$\frac{��}{6}$��+$\frac{1}{2}$+a����������ɵ�a=0���ɵ�f��x��=sin��2x+$\frac{��}{6}$��+$\frac{1}{2}$���ú����ĵ�������ͶԳ����ģ�
��2����ͼ��ƽ�Ƶ�֪ʶ�ɵ�����ƽ��m����λ���ȣ��������Գ����Ƶ�y�ᣮ
��� �⣺��1����f��x��=$\sqrt{3}$sinxcosx+cos2x+a��
��f��x��=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$��1+cos2x��+a��
��f��x��=sin��2x+$\frac{��}{6}$��+$\frac{1}{2}$+a��
��x��[-$\frac{��}{6}$��$\frac{��}{3}$]ʱ��2x+$\frac{��}{6}$��[-$\frac{��}{6}$��$\frac{5��}{6}$]��
sin��2x+$\frac{��}{6}$����[-$\frac{1}{2}$��1]��
����f��x�������ֵ����Сֵ�ĺ�Ϊ1+$\frac{1}{2}$+a+a=$\frac{3}{2}$��
��a=0��
��f��x��=sin��2x+$\frac{��}{6}$��+$\frac{1}{2}$��
��2k��-$\frac{��}{2}$��2x+$\frac{��}{6}$��2k��+$\frac{��}{2}$����k��-$\frac{��}{3}$��x��k��+$\frac{��}{6}$��
��f��x���ĵ�������������[k��-$\frac{��}{3}$��k��+$\frac{��}{6}$]��
�����ݼ�������[k��+$\frac{��}{6}$��k��+$\frac{2��}{3}$]��
��2x+$\frac{��}{6}$=k�У��ɵ�x=-$\frac{��}{12}$+$\frac{1}{2}$k�У�
��Գ������ǣ�-$\frac{��}{12}$+$\frac{1}{2}$k�У�$\frac{1}{2}$������k��Z����
��2����a=-$\frac{1}{2}$ʱ��f��x��=sin��2x+$\frac{��}{6}$����
�Գ���Ϊx=$\frac{��}{6}$+$\frac{1}{2}$k�У���k��Z����
��f��x�����ĸ����Գ���Ϊx=-$\frac{��}{3}$��
m=$\frac{��}{3}$��
���� �����Ǻ�����ʽ�ɻ���������ɵ�a=0���ú����ĵ�������ͶԳ����ģ���ͼ��ƽ�Ƶ�֪ʶ�ɵ�����ƽ��m����λ���ȣ��������Գ����Ƶ�y�ᣮ


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
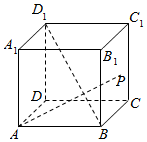 ��ͼ��������ABCD-A1B1C1D1�У���P�ڲ���BCC1B1����߽����˶����������DZ���AP��BD1����֤������P���߶�B1C�ϣ�
��ͼ��������ABCD-A1B1C1D1�У���P�ڲ���BCC1B1����߽����˶����������DZ���AP��BD1����֤������P���߶�B1C�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 17 | C�� | 18 | D�� | 19 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com