
分析 联立直线和双曲线的方程,化为关于x的一元二次方程后利用根与系数关系求出A,B两点的横纵坐标的积,由以AB为直径的圆经过坐标原点得到x1x2+y1y2=0,代入后即可求得m的值.然后利用弦长公式求解即可.
解答 解:联立$\left\{\begin{array}{l}{y=x+m}\\{2{x}^{2}-{y}^{2}=2}\end{array}\right.$,消去y得,x2-2mx-2-m2=0.
∵直线y=x+m与双曲线2x2-y2=2相交于A,B两点,
由△=(-2m)2+4(2+m2)=8+8m2>0,
设A(x1,y1),B(x2,y2).
则x1+x2=2m,x1x2=-2-m2.
所以y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2=2m2-2,
因为以AB为直径的圆经过坐标原点,
即为$\overrightarrow{OA}•\overrightarrow{OB}$=0,
所以x1x2+y1y2=0.
即-2-m2+2m2-2=0,
解得m=±2.
所以m的值是±2.
弦AB的长:$\sqrt{1+{1}^{2}}$|x1-x2|=$\sqrt{2}×$$\sqrt{4{m}^{2}-4(-2-{m}^{2})}$=$\sqrt{2}×$$\sqrt{16+24}$=4$\sqrt{5}$.
点评 本题考查了直线与圆锥曲线的关系,考查了数学转化思想方法,训练了利用数量积判断两个向量的垂直关系,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
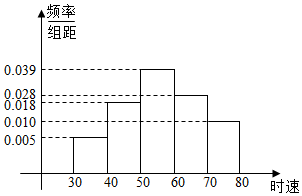
 为检验寒假学生自主学生的效果,级部对某班50名学生各科的检测成绩进行了统计,下面是物理成绩的频率分布直方图,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
为检验寒假学生自主学生的效果,级部对某班50名学生各科的检测成绩进行了统计,下面是物理成绩的频率分布直方图,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com