
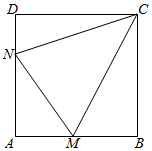
 如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.
如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.分析 (Ⅰ)设∠DCN=∠BCM=θ,由题意利用勾股定理可求CN=CM=$\frac{\sqrt{5}}{2}$,从而可求sinθ=$\frac{\sqrt{5}}{5}$,cosθ=$\frac{2\sqrt{5}}{5}$,∠MCN=$\frac{π}{2}$-2θ,利用诱导公式,二倍角公式即可求∠MCN的余弦值.
(Ⅱ)设∠BCM=α,∠DCN=β,AM=x,AN=y,可求BM=1-x,DN=1-y,tanα=1-x,tanβ=1-y,可得tan(α+β)=$\frac{2-(x+y)}{x+y-xy}$,由x+y+$\sqrt{{x}^{2}+{y}^{2}}$=2,化简得xy=2(x+y)-2,求得tan(α+β)=1,即可得解∠MCN是定值,且∠MCN=$\frac{π}{4}$.
解答 (本题满分为12分)
解:(Ⅰ)当点M,N分别是边AB,AD的中点时,设∠DCN=∠BCM=θ,
CD=BC=1,DN=BM=$\frac{1}{2}$,CN=CM=$\frac{\sqrt{5}}{2}$,sinθ=$\frac{\sqrt{5}}{5}$,cosθ=$\frac{2\sqrt{5}}{5}$,∠MCN=$\frac{π}{2}$-2θ ,
,
所以cos∠MCN=cos($\frac{π}{2}$-2θ)=sin2θ=2sinθcosθ=$\frac{4}{5}$,
所以∠MCN的余弦值是$\frac{4}{5}$.-----------(6分)
(Ⅱ)设∠BCM=α,∠DCN=β,AM=x,AN=y,则BM=1-x,DN=1-y,
在△CBM中,tanα=1-x,在△CDN中,tanβ=1-y,
所以:tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{1-x+1-y}{1-(1-x)(1-y)}$=$\frac{2-(x+y)}{x+y-xy}$,(*)----------(8分)
△AMN的周长为2千米,所以x+y+$\sqrt{{x}^{2}+{y}^{2}}$=2,化简得xy=2(x+y)-2,
代入(*)式,可得tan(α+β)=$\frac{2-(x+y)}{x+y-xy}$=$\frac{2-(x+y)}{x+y-[2(x+y)-2]}$=$\frac{2-(x+y)}{2-(x+y)}$=1,
所以α+β=$\frac{π}{4}$,所以∠MCN是定值,且∠MCN=$\frac{π}{4}$.-----------(12分)
点评 本题主要考查了诱导公式,二倍角公式,勾股定理,两角和的正切函数公式的综合应用,考查了转化思想和数形结合思想,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
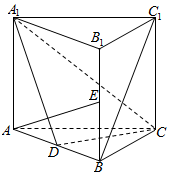 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
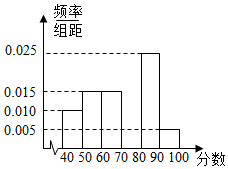 某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
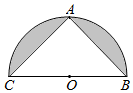 如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )
如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com