
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
分析 作出不等式组对应的平面区域,求出对应区域的面积,利用几何概型的概率公式进行计算即可.
解答  解:作出不等式组对应的区域,则结合A对应正方形ABCD,面积S=2×2=4,
解:作出不等式组对应的区域,则结合A对应正方形ABCD,面积S=2×2=4,
是曲线$y=\sqrt{1-{{({x-1})}^2}}$围成的封闭区域在正方形内为圆的$\frac{1}{4}$,对应的面积S=$\frac{1}{4}$×π×12=$\frac{π}{4}$,
则向区域A上随机投一点P,则点P落入区域B的概率P=$\frac{\frac{π}{4}}{4}$=$\frac{π}{16}$,
故选:B
点评 本题主要考查几何概型的概率的计算,作出对应的区域,求出对应的面积,利用几何概型的概率公式是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | α∥β | B. | α⊥β | C. | α,β相交但不垂直 | D. | 以上均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
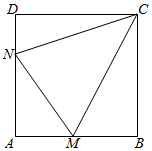 如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.
如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
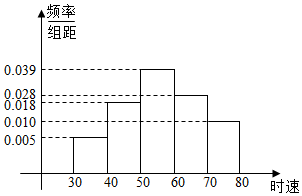
 为检验寒假学生自主学生的效果,级部对某班50名学生各科的检测成绩进行了统计,下面是物理成绩的频率分布直方图,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
为检验寒假学生自主学生的效果,级部对某班50名学生各科的检测成绩进行了统计,下面是物理成绩的频率分布直方图,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com