
分析 (1)通过设{an}的公差为d,利用a3a5=3a7与S3=9联立方程组,进而可求出首项和公差,进而可得结论
(2)通过(1)裂项、并项相加可知Tn=$\frac{n}{2(n+2)}$,利用基本不等式即得结论.
解答 解:(1)设{an}的公差为d,
∵a3a5=3a7,S3=9,
∴$\left\{\begin{array}{l}({{a_1}+2d})({{a_1}+4d})=3({{a_1}+6d})\\ 3{a_1}+\frac{3×2}{2}d=9\end{array}\right.$,
解得$\left\{\begin{array}{l}d=0\\{a_1}=3\end{array}\right.$(舍去)或$\left\{\begin{array}{l}d=1\\{a_1}=2\end{array}\right.$,
∴an=2+(n-1)×1=n+1;
(2)∵$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{({n+1})({n+2})}}=\frac{1}{n+1}-\frac{1}{n+2}$,
∴${T_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$
=$({\frac{1}{2}-\frac{1}{3}})+({\frac{1}{3}-\frac{1}{5}})+…+({\frac{1}{n+1}-\frac{1}{n+2}})$
=$\frac{1}{2}-\frac{1}{n+2}$
=$\frac{n}{{2({n+2})}}$,
∴$\frac{T_n}{{{a_{n+1}}}}=\frac{n}{{2{{({n+2})}^2}}}=\frac{n}{{2({{n^2}+4n+4})}}=\frac{1}{{2({n+4+\frac{4}{n}})}}≤\frac{1}{{2({4+2\sqrt{n•\frac{4}{n}}})}}=\frac{1}{16}$,
当且仅当 $n=\frac{4}{n}$,即n=2时“=”成立,
即当n=2时,$\frac{T_n}{{{a_{n+1}}}}$取得最大值$\frac{1}{16}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,涉及基本不等式等基础知识,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
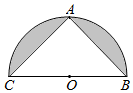 如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )
如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中用X表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中用X表示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com