
分析 (1)求导数,确定切线的斜率,可得切线方程;
(2)求出过点P,Q且与抛物线分别相切的直线方程,可得M的坐标,利用等比数列的定义进行证明.
解答 (1)解:由题意,y=2$\sqrt{x}$,y′=$\frac{1}{\sqrt{x}}$,x=1,y′=1,
∴过点P且与抛物线相切的直线方程为y-2=x-1,即x-y+1=0;
(2)证明:设P(x1,y1),Q(x2,y2),则过P的切线方程为y-y1=$\frac{1}{\sqrt{{x}_{1}}}$(x-x1),即y=$\frac{1}{\sqrt{{x}_{1}}}$x+$\sqrt{{x}_{1}}$,
同理过Q的切线方程为y=$\frac{1}{\sqrt{{x}_{2}}}$x+$\sqrt{{x}_{2}}$,可得M($\sqrt{{x}_{1}{x}_{2}}$,$\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$),
∴|PF|=x1+1,|QF|=x2+1,|MF|2=($\sqrt{{x}_{1}{x}_{2}}$-1)2+($\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$)2,
∴|MF|2=|PF||QF|,
∴|PF|,|MF|,|QF|依次成等比数列.
点评 本题考查抛物线的切线方程,考查等比数列的证明,综合性强.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
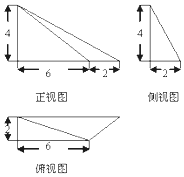
| A. | $\frac{56}{3}$ | B. | $\frac{112}{3}$ | C. | $\frac{119}{3}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若(a-2)(b-3)≠0,则a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,则a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,则a≠2或b≠3 | D. | 若(a-2)(b-3)=0,则a≠2且b≠3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com