Question

1．在△ABC中，∠A=$\frac{3π}{4}$，AB=6，AC=3$\sqrt{2}$，点D在BC边上，AD=BD，求AD的长．

Answer 1

分析 由已知及余弦定理可解得BC的值，由正弦定理可求得sinB，从而可求cosB，过点D作AB的垂线DE，垂足为E，由AD=BD得：cos∠DAE=cosB，即可求得AD的长．

解答 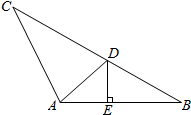解：∵∠A=$\frac{3π}{4}$，AB=6，AC=3$\sqrt{2}$，
∴在△ABC中，由余弦定理可得：BC²=AB²+AC²-2AB•ACcos∠BAC=90．
∴BC=3$\sqrt{10}$…4分
∵在△ABC中，由正弦定理可得：$\frac{AC}{sinB}=\frac{BC}{sin∠BAC}$，
∴sinB=$\frac{\sqrt{10}}{10}$，
∴cosB=$\frac{3\sqrt{10}}{10}$…8分
∵过点D作AB的垂线DE，垂足为E，由AD=BD得：cos∠DAE=cosB，
∴Rt△ADE中，AD=$\frac{AE}{cos∠DAE}$=$\frac{3}{cosB}$=$\sqrt{10}$…12分

点评 本题主要考查了正弦定理，余弦定理在解三角形中的应用，属于基本知识的考查．