
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源:不详 题型:解答题
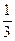 )是函数
)是函数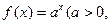 且
且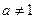 )的图象上一点,等比数列
)的图象上一点,等比数列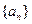 的前n项和为
的前n项和为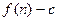 ,数列
,数列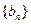
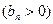 的首项为c,且前n项和
的首项为c,且前n项和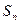 满足
满足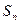 -
-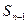 =
=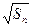 +
+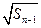 (n
(n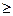 2).
2).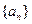 和
和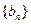 的通项公式;
的通项公式;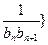 前n项和为
前n项和为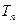 ,问
,问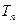 >
>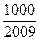 的最小正整数n是多少?
的最小正整数n是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
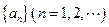 是等差数列,且公差为
是等差数列,且公差为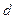 ,若数列
,若数列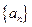 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.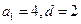 ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”;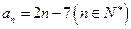 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么?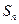 是数列
是数列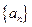 的前
的前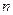 项和,若公差
项和,若公差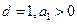 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使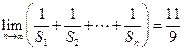 ;若存在,求
;若存在,求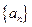 的通项公式,若不存在,说明理由.
的通项公式,若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
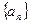 是公差为
是公差为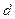
 的等差数列,数列
的等差数列,数列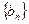 是公比为
是公比为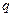 的(q∈R)的等比数列,若函数
的(q∈R)的等比数列,若函数 ,且
,且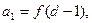
 ,
,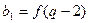 ,
,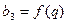 ,
,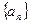 和
和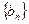 的通项公式;
的通项公式;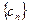 的前n项和为
的前n项和为 ,对一切
,对一切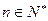 ,都有
,都有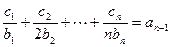 成立,求
成立,求
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
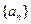 的前n项和为
的前n项和为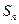 ,数列
,数列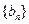 满足:
满足: 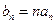 ,且数列
,且数列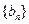 的前
的前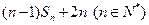 .
.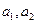 的值;
的值;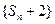 是等比数列;
是等比数列;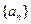 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列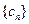 ,若
,若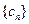 的前n项和为
的前n项和为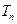 ,求证:
,求证: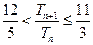 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com