
| A. | 大于零 | B. | 小于零 | C. | 等于零 | D. | 不能确定 |
分析 由三角形内角和定理得到A+B+C=π,表示出B,代入原式利用诱导公式化简,根据B为钝角,得到A+C的范围,利用正弦函数的单调性确定出原式的正负即可.
解答 解:∵在△ABC中,A+B+C=π,
∴B=π-(A+C),
∴sinB-sinA=sin[π-(A+C)]-sinA=sin(A+C)-sinA,
∵B为钝角,∴A<A+C<$\frac{π}{2}$,
∵正弦函数在(0,$\frac{π}{2}$)是增函数,
∴sin(A+C)>sinA,即sin(A+C)-sinA>0,
则sinB-sinA大于零,
故选:A.
点评 此题考查了三角函数值的符号,诱导公式,以及正弦函数的单调性,熟练掌握公式及性质是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 360 | B. | 90 | C. | 540 | D. | 2160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
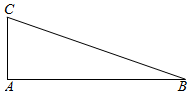 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=$\frac{\sqrt{2}}{2}$,一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=$\frac{\sqrt{2}}{2}$,一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com