
分析 (Ⅰ)根据正切函数的性质可得x+$\frac{π}{3}$≠$\frac{π}{2}+kπ$,k∈Z,可得定义域.利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期.
(Ⅱ)x∈[-$\frac{π}{2}$,0]上时,求出内层函数的取值范围,结合三角函数的图象和性质,可求出f(x)的最大值和最小值.
解答 解:(Ⅰ)由题意,函数f(x)=cosx•tan(x+$\frac{π}{3}$)cos(x+$\frac{π}{3}$)-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$.
根据正切函数的性质可得x+$\frac{π}{3}$≠$\frac{π}{2}+kπ$,k∈Z,
可得:x≠$\frac{π}{6}+kπ$,k∈Z,
函数f(x)的定义域为{x∈R|x≠$\frac{π}{6}+kπ$,k∈Z}.
将函数f(x)化简可得:f(x)=cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$sinxcosx+$\frac{\sqrt{3}}{2}$cos2x-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{4}$.
=$\frac{1}{4}$sin2x-$\frac{\sqrt{3}}{2}$cos2x$+\frac{\sqrt{3}}{4}$
=$\frac{1}{4}$sin2x-$\frac{\sqrt{3}}{2}(\frac{1}{2}+\frac{1}{2}cos2x)$$+\frac{\sqrt{3}}{4}$
=$\frac{1}{4}$sin2x-$\frac{\sqrt{3}}{4}$cso2x
=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$.
(Ⅱ)由(Ⅰ)可知f(x)=$\frac{1}{2}$sin(2x-$\frac{π}{3}$)
当x∈[-$\frac{π}{2}$,0]上时,
可得:2x-$\frac{π}{3}$∈[$-\frac{4π}{3}$,$-\frac{π}{3}$].
当2x-$\frac{π}{3}$=$-\frac{π}{2}$时,f(x)取得最小值为-$\frac{1}{2}$.
当2x-$\frac{π}{3}$=$-\frac{4π}{3}$时,f(x)取得最大值为$\frac{\sqrt{3}}{4}$.
故得函数f(x)在x∈[-$\frac{π}{2}$,0]上的最大值为$\frac{\sqrt{3}}{4}$,最小值为$-\frac{1}{2}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{30}}}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 9π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
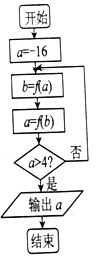 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )| A. | 16 | B. | 8 | C. | 216 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | $1+\sqrt{2}$ | C. | $1+\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com