
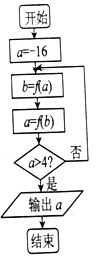
 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )| A. | 16 | B. | 8 | C. | 216 | D. | 28 |
分析 框图在输入a=-16后,对循环变量a的大小进行判断,直至满足条件a>4算法结束.
解答 解:模拟执行程序框图,可得
a=-16≤0,
执行循环体,b=log${\;}_{\frac{1}{2}}$16=14<0,a=log${\;}_{\frac{1}{2}}$4=-2<0,
不满足条件a>4,执行循环体,b=log${\;}_{\frac{1}{2}}$2=-1<0,a=log${\;}_{\frac{1}{2}}$1=0,
不满足条件a>4,执行循环体,b=2°=1>0,a=21=2,
不满足条件a>4,执行循环体,b=22=4>0,a=24=16,
满足条件a>4,退出循环,输出a的值为16.
故选:A.
点评 本题考查了程序框图,考查了循环结构中的直到型循环,直到型循环是先执行后判断,此题是基础题.


科目:高中数学 来源: 题型:选择题
| A. | a≤-1 | B. | a<-1 | C. | a>1 | D. | a≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}+\frac{3}{5}i$ | B. | $-\frac{4}{5}-\frac{3}{5}i$ | C. | $-\frac{4}{25}+\frac{3}{25}i$ | D. | $-\frac{4}{25}-\frac{3}{25}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 平面内的小圆形按照如图中的规律排列,每个图中的圆的个数构成一个数列{an},则系列结论正确的是( )
平面内的小圆形按照如图中的规律排列,每个图中的圆的个数构成一个数列{an},则系列结论正确的是( )| A. | ①②④ | B. | ①③④ | C. | ①② | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2017}$ | B. | $-\frac{1}{2017}$ | C. | $\frac{1}{4034}$ | D. | $-\frac{1}{4034}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com