
| A. | $-\frac{4}{5}+\frac{3}{5}i$ | B. | $-\frac{4}{5}-\frac{3}{5}i$ | C. | $-\frac{4}{25}+\frac{3}{25}i$ | D. | $-\frac{4}{25}-\frac{3}{25}i$ |
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:解答题
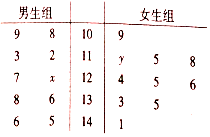 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
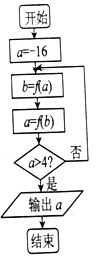 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )| A. | 16 | B. | 8 | C. | 216 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
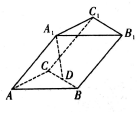 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | i | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com