
| A. | $\frac{1}{2017}$ | B. | $-\frac{1}{2017}$ | C. | $\frac{1}{4034}$ | D. | $-\frac{1}{4034}$ |
分析 利用赋值法,令x=0求得a0,令x=$\frac{1}{2}$求得$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2017}}{{2}^{2017}}$,再利用二项展开式的通项公式求出a1,从而求出$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2017}}}}{{{2^{2017}}{a_1}}}$的值.
解答 解:(2x-1)2017=a0+a1x+a2x2+…+a2017x2017中,
令x=0,可得-1=a0;
令x=$\frac{1}{2}$,可得0=-1+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2017}}{{2}^{2017}}$,
∴$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2017}}{{2}^{2017}}$=1;
又(2x-1)2017展开式中,通项公式为:
Tr+1=${C}_{2017}^{r}$•(2x)2017-r•(-1)r,
令2017-r=1,解得r=2016;
∴(2x-1)2017展开式中,含x项的系数为:
a1=2${C}_{2017}^{2016}$=4034,
∴$\frac{1}{2}+\frac{a_2}{{{2^2}{a_1}}}+\frac{a_3}{{{2^3}{a_1}}}+…+\frac{{{a_{2017}}}}{{{2^{2017}}{a_1}}}$=$\frac{1}{{a}_{1}}$=$\frac{1}{4034}$.
故选:C.
点评 本题考查了二项式定理的应用问题,也考查了推理能力与计算能力,是中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
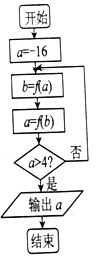 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )| A. | 16 | B. | 8 | C. | 216 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | $1+\sqrt{2}$ | C. | $1+\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$ | B. | 1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com