
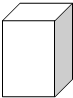
 一款底面为正方形的长方体无盖金属容器(忽略其厚度),如图所示,当其容积为500cm3时,问容器的底面边长为多少时,所使用材料最省?
一款底面为正方形的长方体无盖金属容器(忽略其厚度),如图所示,当其容积为500cm3时,问容器的底面边长为多少时,所使用材料最省? 分析 设底面边长为xcm,高为ycm,根据体积公式用x表示出y,代入表面积公式得出表面积S关于x的函数,利用导数求出此函数的极小值点即可.
解答 解:设长方体底面边长为xcm,高为ycm,
则x2y=500,∴y=$\frac{500}{{x}^{2}}$.
∴长方体的表面积(不包括上底面)为S(x)=x2+4xy=x2+$\frac{2000}{x}$,
∴S′(x)=2x-$\frac{2000}{{x}^{2}}$=$\frac{2({x}^{3}-1000)}{{x}^{2}}$,
令S′(x)=0得x=10,
当0<x<10时,S′(x)<0,当x>10时,S′(x)>0,
∴S(x)在(1,10]上单调递减,在(10,+∞)上单调递增,
∴当x=10时,S(x)取得最小值.
答:当容器底面边长为10cm时,所使用材料最省.
点评 本题考查了导数与函数最值的关系,函数最值的应用,属于中档题.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,e4) | D. | (e4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
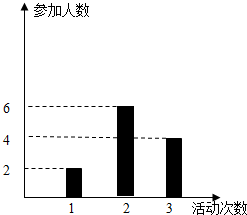 某城市号召中学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该城市某学校学生会共有12名学生,他们参加活动的次数统计如图所示.
某城市号召中学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该城市某学校学生会共有12名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com