
分析 (1)利用矩阵的加法、乘法,即可写出PQ=M+N所表示的关于x、y的二元一次方程组;
(2)用行列式的方法,分类讨论解二元一次方程组.
解答 解:(1)由PQ=M+N,得$({\begin{array}{l}{mx+y}\\{3mx-my}\end{array}})=({\begin{array}{l}{-1}\\{2m+3}\end{array}})$,方程组为$\left\{\begin{array}{l}{mx+y=-1}\\{3mx-my=2m+3}\end{array}\right.$;(3分)
(2)$D=|{\begin{array}{l}m&1\\{3m}&{-m}\end{array}}|=-m(m+3)$,${D_x}=|{\begin{array}{l}{-1}&1\\{2m+3}&{-m}\end{array}}|=-(m+3)$,${D_y}=|{\begin{array}{l}m&{-1}\\{3m}&{2m+3}\end{array}}|=2m(m+3)$(5分)
1°当m≠0,且m≠-3时,D≠0,方程组有唯一解$\left\{{\begin{array}{l}{x=\frac{1}{m}}\\{y=-2}\end{array}}\right.$;
2°当m=0时,D=0,但Dx≠0,方程组无解;
3°当m=-3时,D=Dx=Dy=0,方程组有无穷多解$\left\{\begin{array}{l}{x=t}\\{y=3t-1}\end{array}\right.$(t∈R).(8分)
点评 本题考查矩阵的加法、乘法,考查用行列式解二元一次方程组,考查学生的计算能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
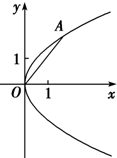 如图,在平面直角坐标系xoy中,抛物线C的顶点在原点,经过点A(2,4),其焦点F在x轴上.
如图,在平面直角坐标系xoy中,抛物线C的顶点在原点,经过点A(2,4),其焦点F在x轴上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2a+b}{1-a+b}$ | B. | $\frac{2a+b}{1+a+b}$ | C. | $\frac{a+2b}{1-a+b}$ | D. | $\frac{a+2b}{1+a+b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{4}{3}$) | B. | [0,$\frac{4}{3}$] | C. | (-4,$\frac{4}{3}$) | D. | [-4,$\frac{4}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{1}{2}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{1}{2}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com