
| A. | $\frac{2a+b}{1-a+b}$ | B. | $\frac{2a+b}{1+a+b}$ | C. | $\frac{a+2b}{1-a+b}$ | D. | $\frac{a+2b}{1+a+b}$ |
分析 利用对数的运算性质,用lg2和lg3表示lg12和lg15,再把所给的值代入即可.
解答 解:$\frac{lg12}{lg15}$=$\frac{lg(3×4)}{lg(3×5)}=\frac{lg3+lg4}{lg3+lg5}$=$\frac{lg3+2lg2}{lg3+lg\frac{10}{2}}=\frac{lg3+2lg2}{lg3+1-lg2}$,
∵lg2=a,lg3=b,
∴$\frac{lg12}{lg15}$=$\frac{2a+b}{1-a+b}$,
故选:A.
点评 本题考查了对数的运算性质,对于这类有条件的求值问题,一般需要把所给的式子用已知的条件表示出来,是基础题.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
| 支持 | 保留 | 不支持 | |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
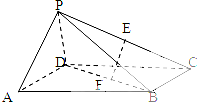
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\frac{n}{2n+1}$(n∈N+) | B. | an=$\frac{n}{2n-1}$(n∈N+) | C. | an=$\frac{n}{2n+3}$(n∈N+) | D. | an=$\frac{n}{2n-3}$(n∈N+) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com